7．恒成立问题

例7：当具有什么关系时，二次函数的函数值恒大于零？恒小于零？

变式1：已知函数 f (x) = lg (a x ² + 2x + 1) ．

(I)若函数 f (x) 的定义域为 R，求实数 a 的取值范围； a>1

(II)若函数 f (x) 的值域为 R，求实数 a 的取值范围．　 [0,1]

6．值域

例6：求二次函数在下列定义域上的值域：

(1)定义域为；(2) 定义域为．

{0，4}　　　　　　　　　　　　 [-20,4]

变式1：函数的值域是

变式2：函数y=cos2x+sinx的值域是[-2,]．

5．奇偶性

例5：已知函数是定义在R上的奇函数，当≥0时，．画出函数的图像，并求出函数的解析式．x<0,f(x)= x(1-x)

变式1：若函数是偶函数，则在区间上是 增　 函数　　　

4．最值

例4已知函数在区间[0,m]上有最大值3，最小值2，则m的取值范围是　 [1,2]

变式1：已知函数在区间[0,2]上的最小值为3，求a的值．1-,

3．单调性

例3：已知函数，．求的单调区间及其最值．　 增[2，4]　 [0，8]

变式1：已知函数在区间内单调递减，则a的取值范围是　　 a≤-3

2、图像特征

例2：将函数配方，确定其对称轴，顶点坐标，求出它的单调区间及最大值或最小值，并画出它的图像．

变式1：函数对任意的x均有，那么、、的大小关系是< <

1、解析式、待定系数法

例1．若，且，，求的值．8

变式1：若二次函数的图像的顶点坐标为，与y轴的交点坐标为(0,11)，则 　　　　　　　　　　　　　　　

变式2：若的图像x=1对称，则c=2．　　　　 f(x)=3x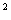-12x+11

9．　已知函数的图象与两坐标轴都无公共点，且其图象关于y轴对称，求n的值，并画出函数的图象．　 -4

典型例题

8. 求下列函数的定义域、值域：

①; 　[-1,-1] 　　　②　　 (-1,5)　 [-3,+)

7.求函数的单调减区间。(6,+)