
教学 环节 |
教学内容 |
师生互动 |
设计意图 |
||||||||||||||||||||||||
提出 问题 |
观察一次函数f (x) = x的图象: 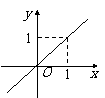   函数f (x) = x的图象特征由左到右是上升的. |
师:引导学生观察图象的升降. 生:看图. 并说出自己对图象 的直观认识.  师:函数值是由自变量的增大而增大,或由自变量的增大而减小,这种变化规律即函数的单调性. |
在函数图象的观察中获取函数单调性的直观认识. |
||||||||||||||||||||||||
|
引入深题 |
观察二次函数f (x) = x2 的图象: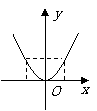   函数f (x) = x2 在y轴左侧是下降的,在y轴右侧是上升的.  列表: 
x∈(–∞,0]时,x增大,f (x)减少,图象下降. x∈(0,+∞)时,x增大,f (x)也增大, 图象上升. |
师:不同函数,其图象上升、下降规律不同. 且同一函数在不同区间上的变化规律也不同. 这是“形”的方面,从“数”的方面如何反映. 生:函数作图时列表描点过程中,从列表的数据变化可知自变量由 – 4到0变化,函数值随着变小;而自变量由0到4变化,函数值随着自变量的变大而变大.  师:表格数值变化的一般规随是:自变量x增大,函数值y也增大,函数图象上升,称函数为增函数;自变量x增大,函数值y反而减少,函数图象下降. 称函数为减函数. |
体会同一函数在不同区间上的变化差异. 引导学生从“形变”过渡到“数变”. 从定性分析到定量分析. |
||||||||||||||||||||||||
|
形成概念 |
函数单调性的概念 一般地,设函数f (x)的定义域为I:  如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f (x1)<f (x2),那么就说函数f (x)在区间D上是增函数(increasing function);  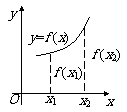   如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2,当x1<x2时,都有f (x1)>f (x2),那么就说函数f (x)在区间D上是减函数(decreasing function).    |
师:增函数、减函数的函数值随自变量的变化而变化怎么用数学符号表示呢? 师生合作:  对于函数f (x) = x2 在区间(0,+∞)上. 任取x1、x2. 若x1<x2,则f (x1)<f (x2),即x12<x22.  师:称f (x) = x2在(0,+∞)上为增函数. |
由实例探究规律从而获得定义的数学符号表示. |
||||||||||||||||||||||||
应用 举例 |
例1 如图是定义在区间[–5,5]上的函数y = f (x),根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?   训练题1:  (1)请根据下图描述某装配线的生产率与生产线上工人数量间的关系.    (2)整个上午(8∶00-12∶00)天气越来越暖,中午时分(12∶00-13∶00)一场暴风雨使天气骤然凉爽了许多. 暴风雨过后,天气转暖,直到太阳落山(18∶00)才又开始转凉. 画出这一天8∶00-20∶00期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.  (3)根据下图说出函数单调区间,以及在每一单调区间上,函数是增函数还是减函数.  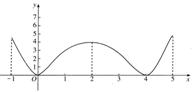  例2 物理学中的玻意耳定律  (k为正常数) 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大. 试用函数的单调性证明之. (k为正常数) 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大. 试用函数的单调性证明之.训练题2:证明函数f (x) = –2x +1在R上是减函数. |
师:投影例1. 生:合作交流完成例1. 师:引导学生完成教材P36练习的第1题、第2题. 师:投影训练题1 生:学生通过合作交流自主完成. 例1[解]:y= f (x)的单调区间有[–5,–2),[–2,1),[1,3),[3,5]. 其中y = f (x) 在区间[–5,–2),[1,3)上是减函数,在区间[–2,1),[3,5]上是增函数. 训练题1 答案:(1)在一定范围内,生产效率随着工人数的增加而提高,当工人数达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率又随着工人的增加而降低. 由此可见,并非是工人越多,生产效率就越高. (2) 增区间为[8,12],[13,18];减区间为:[12,13],[18,20]. (3)函数在[–1,0]上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]是增函数. 师:打出例2,请学生阐明应用定义证明(判定)并总结证明单调性的基本步骤. 生:学生代表板书证明过程,教师点评. 例2 分析:按题意,只要证明函数  在区间(0,+∞)上是减函数即可. 在区间(0,+∞)上是减函数即可.证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1<V2,即 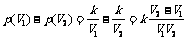 . .由V1,V2∈(0,+∞),得V1V2>0. 由V1<V2,得V2 – V1>0. 又k>0,于是 p (V1) – p (V2)>0, 即 p (V1) >p (V2). 所以,函数  ,V?(0,+∞)是减函数,也就是说,当体积V减小时,压强p将增大. ,V?(0,+∞)是减函数,也就是说,当体积V减小时,压强p将增大.师:投影训练题2 生:自主完成 训练题2 证明:任取x1,x2∈R,且x1<x2, 因为f (x1) – f (x2) =2 (x2 –x1)>0, 即f (x1)>f (x2), 所以f (x) = –2x +1在R上是减函数. |
掌握利用图象划分函数单调区间的方法. 掌握单调性证明步骤及原理.内化定义,强化划分单调区间的方法. 强化记题步骤与格式. |
||||||||||||||||||||||||
|
归纳 小结 |
1°体会函数单调性概念的形成过程. 2°单调性定义. 3°利用图象划分单调区间. 4°利用定义证明单调性步骤. |
师生合作:回顾单调性概念的形式与发展. 师:阐述单调性的意义与作用. |
反思回顾 整理知识,提升能力. |
||||||||||||||||||||||||
|
课后 练习 |
1.3第一课时 习案 |
学生独立完成 |
巩固知识 培养能力 |
备选例题:
例1 证明函数f (x) =3x +2在R上是增函数.
[证明]设任意x1、x2?R,且x1<x2,
则f (x1) – f (x2) = (3x1 +2) – (3x2 +2) = 3(x1–x2).
由x1<x2得x1 –x2<0. ∴f (x1) – f (x2)<0,即f (x1)<f (x2).
∴f (x) =3x +2在R上是增函数.
例2 证明函数f (x) =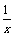 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.
[证明]设任意x1、x2?(0,+ ∞)且x1<x2,
则f (x1)
– f (x2) = ,
,
由x1,x2?(0,+∞)得,x1x2>0,又x1<x2,得x2 – x1>0,
∴f (x1) – f (x2) >0,即f (x1)<f (x2).
∴f (x) =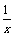 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.
讨论式教学法. 在老师的引导下,学生在回顾旧知,细心观察、认真分析、严谨论证的学习过程中生疑与析疑,合作与交流,归纳与总结的过程中获得新知,从而形成概念,掌握方法.
重点:理解增函数、减函数的概念;难点:单调性概念的形成与应用.
3.情感、态度与价格观
在形与数的结合中感知数学的内在美,在图形语言、自然语言、数学语言的转化中感知数学的严谨美.
2.过程与方法
由一元一次函数、一元二次函数的图象,让学生从图象获得“上升”“下降”的整体认识. 利用函数对应的表格,用自然语言描述图象特征“上升”“下降”最后运用数学符号将自然语言的描述提升到形式化的定义,从而构造函数单调性的概念.
1.知识与技能
(1)理解函数单调性的定义、明确增函数、减函数的图象特征.
(2)能利用函数图象划分函数的单调区间,并能利用定义进行证明.
25、答:题中的观点是不科学的。
(1)在我国社会主义初级阶段,公有制为主体,多种所有制经济共同发展的基本经济制度决定了我国必须实行以按劳分配为主体、多种分配方式并存的分配制度,把按劳分配和按生产要素分配结合起来。
(2)允许和鼓励生产要素按贡献参与分配,能激励人们更有效地使用生产要素,提高生产要素的利用效率,发展社会主义的生产力,但同时也会造成社会成员之间的收入差别。
(3)在社会主义初级阶段,我们把按劳分配和按生产要素分配结合起来,坚持效率优先,兼顾公平原则,一方面我们要允许和鼓励一部分人先富起来,另一面国家对社会成员之间的收入差距加以适当调节,有效地防止两极分化。所以,允许和鼓励生产要素按贡献参与分配不会导致两极分化。
24.答案(1)有利于提高农民的购买力,扩大内需,推动我国经济的健康发展。有利于提高农民的生活水平,维护社会的公平,促进社会稳定。有利于统筹城乡发展,逐步实现共同富裕,全面构建和谐社会。
(2)措施:加强国家宏观调控,采取多种手段调节收入差距,坚持效率优先,更加注重社会公平;坚持“多予少取”,增加财政对农业和农村的投入,促进农业发展和农民增收,切实减轻农民负担;完善分配制度和社会保障制度,切实维护广大农民的合法权益。
23、答案:(1)材料反映了我国实行以按劳分配为主体、多种分配方式并存的分配制度。
(2)我国实施这一制度应坚持效率优先、兼顾公平的原则。这个原则允许一部分人通过诚实劳动、合法经营先富起来,先富带动后富,达到共同富裕。同时,又通过各种政策,调节过高收入,依法保护合法收入,取缔非法收入,整顿不合理收人,保障低收入者的基本生活,尽可能实现社会公平、共同富裕。收入过分悬殊就背离了社会主义的根本目标。
26、(1)这家银行的性质是:以银行利润为主要经营目标的金融机构。吸收存款、发放贷款、办理结算等业务。(2)第一,可以为企业提供资金支持。第二,能为企业生产经营提供决策依据。第三,对企业的生产经营活动进行监督管理,提高其经济效益。
第七课主观题答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com