
10. 解析:设圆心坐标为(m,2m),圆的半径为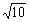 ,所以圆心到直线x-y=0的距离为
,所以圆心到直线x-y=0的距离为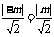
由半径、弦心距、半径的关系得
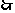 所求圆的方程为
所求圆的方程为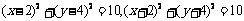
9. x+y-4=0
解析:已知圆的方程为(x-2)2+y2=9,可知圆心C的坐标是(2,0),又知AB弦的中点是P(3,1),所以kCP=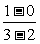 =1,而AB垂直CP,所以kAB=-1.故直线AB的方程是x+y-4=0。
=1,而AB垂直CP,所以kAB=-1.故直线AB的方程是x+y-4=0。
8. 
解析:圆的圆心为(-1,0),如图:

∴kx-y+2=0
当斜率存在时,设切线方程为y=kx+2
∴圆心到切线的距离为 =1
=1
∴k= ,即tanα=
,即tanα=
当斜率不存在时,直线x=0是圆的切线
又∵两切线的夹角为∠α的余角
∴两切线夹角的正切值为
7. 2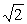
解析:∵点P在直线3x+4y+8=0上。如图:
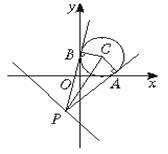
∴设P(x,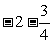 x),C点坐标为(1,1),
x),C点坐标为(1,1),
S四边形PACB=2S△PAC=2· ·|AP|·|AC|=|AP|·|AC|=|AP|
·|AP|·|AC|=|AP|·|AC|=|AP|
∵|AP|2=|PC|2-|AC|2=|PC|2-1
∴当|PC|最小时,|AP|最小,四边形PACB的面积最小。
∴|PC|2=(1-x)2+(1+2+ x)2=
x)2=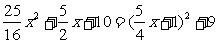
∴|PC|min=3 ∴四边形PACB面积的最小值为2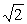 。
。
6. (0, )
)
解析:圆心(2,3)到直线y=kx+2的距离d=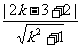
依题意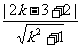 <1 解得:0<k<
<1 解得:0<k<
5. B
解析:圆心坐标为(0,0),半径为1。因为直线和圆相切。利用点到直线距离公式得:d=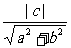 =1,即a2+b2=c2。所以,以|a|,|b|,|c|为边的三角形是直角三角形。
=1,即a2+b2=c2。所以,以|a|,|b|,|c|为边的三角形是直角三角形。
4. C
解析:圆x2+y2+4x+3=0化为标准式(x+2)2+y2=1,圆心C(-2,0)。设过原
点的直线方程为y=kx,即kx-y=0。由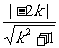 =1,解得k=±
=1,解得k=± ,∵切点在第三象限,∴k>0,所求直线方程为y=
,∵切点在第三象限,∴k>0,所求直线方程为y= x。
x。
3. C
解析:将两圆方程分别配方得(x-1)2+y2=1和x2+(y-2)2=4,两圆圆心分别为O1(1,0),O2(0,2),r1=1,r2=2,|O1O2|= ,
,
又1=r2-r1<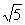 <r1+r2=3,故两圆相交,所以应选C。
<r1+r2=3,故两圆相交,所以应选C。
2. A
解析:圆的标准方程为:(x-1)2+(y-2)2=5。圆过坐标原点。
直线l将圆平分,也就是直线l过圆心C(1,2),从图看到:
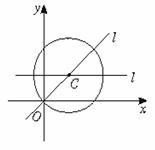
当直线过圆心与x轴平行时,或者直线同时过圆心与坐标原点时都不通过第四象限,并且当直线l在这两条直线之间变化时都不通过第四象限。当直线l过圆心与x轴平行时,k=0,当直线l过圆心与原点时,k=2。∴当k∈[0,2]时,满足题意。
1. A
解析:由圆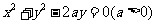 的圆心
的圆心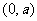 到直线
到直线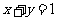 大于
大于 ,且
,且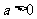 ,选A。
,选A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com