
通过让学生观察、思考、交流、讨论、发现对数函数的图象的特点.
2、难点:底数a对图象的影响.
1、重点:
(1)对数函数的定义、图象和性质;
(2)对数函数性质的初步应用.
3.情感、态度与价值观
(1)通过学习对数函数的概念、图象和性质,使学生体会知识之间的有机联系,激发学生的学习兴趣.
(2)在教学过程中,通过对数函数有关性质的研究,培养观察、分析、归纳的思维能力以及数学交流能力,增强学习的积极性,同时培养学生倾听、接受别人意见的优良品质.
2.过程与方法
(1)培养学生数学交流能力和与人合作精神.
(2)用联系的观点分析问题.通过对对数函数的学习,渗透数形结合的数学思想.
1.知识技能
(1)理解对数函数的概念.
(2)掌握对数函数的性质.了解对数函数在生产实际中的简单应用.
教学 环节 |
教学内容 |
师生互动 |
设计意图 |
||||||||||||
复习 引入  |
复习:对数的定义及对数恒等式  ( (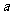 >0,且 >0,且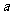 ≠1,N>0), ≠1,N>0), 指数的运算性质.    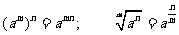  |
学生口答,教师板书. |
对数的概念和对数恒等式是学习本节课的基础,学习新知前的简单复习,不仅能唤起学生的记忆,而且为学习新课做好了知识上的准备. |
||||||||||||
提出 问题 |
探究:在上课中,我们知道,对数式可看作指数运算的逆运算,你能从指数与对数的关系以及指数运算性质,得出相应的对数运算性质吗?如我们知道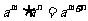 ,那 ,那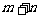 如何表示,能用对数式运算吗? 如何表示,能用对数式运算吗? 如:  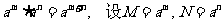 . . 于是 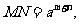 由对数的定义得到 由对数的定义得到 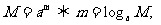  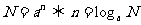  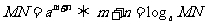  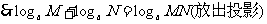  即:同底对数相加,底数不变,真数相乘  提问:你能根据指数的性质按照以上的方法推出对数的其它性质吗?  |
学生探究,教师启发引导. |
|
||||||||||||
概念 形成 |
(让学生探究,讨论) 如果  >0且 >0且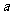 ≠1,M>0,N>0,那么: ≠1,M>0,N>0,那么: (1) 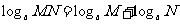  (2) 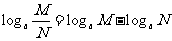  (3) 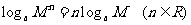  证明:  (1)令 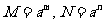  则: 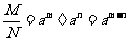  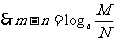  又由 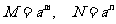  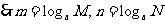  即: 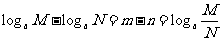  (3)  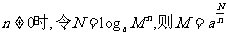  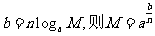  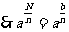  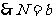  即 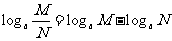  当  =0时,显然成立. =0时,显然成立. 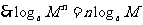  |
 让学生多角度思考,探究,教师点拨.  让学生讨论、研究,教师引导. |
让学生明确由“归纳一猜想”得到的结论不一定正确,但是发现数学结论的有效方法,让学生体会“归纳一猜想一证明”是数学中发现结论,证明结论的完整思维方法,让学生体会回到最原始(定义)的地方是解决数学问题的有效策略.通过这一环节的教学,训练学生思维的广阔性、发散性,进一步加深学生对字母的认识和利用,体会从“变”中发现规律.通过本环节的教学,进一步体会上一环节的设计意图. |
||||||||||||
概念 深化 |
合作探究: 1. 利用对数运算性质时,各字母的取值范围有什么限制条件?    2. 性质能否进行推广?     |
(师组织,生交流探讨得出如下结论) 底数a>0,且a≠1,真数M>0,N>0;只有所得结果中对数和所给出的数的对数都存在时,等式才能成立.  (生交流讨论)  性质(1)可以推广到n个正数的情形,即 loga(M1M2M3…Mn) =logaM1+logaM2 +logaM3+… +logaMn(其中a>0,且a≠1,M1、M2、M3…Mn>0). |
|
||||||||||||
|
应用 举例 |
例1 用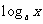 , ,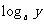 , ,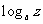 表示下列各式 表示下列各式(1) 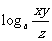 (2) 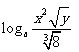 例2 求下列各式的值. (1) 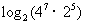 (2) 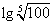 例3计算: (1)lg14-2lg 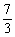 +lg7-lg18; +lg7-lg18;(2) 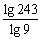 ; ;(3) 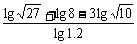 . .课本P79练习第1,2,3. 补充练习:若a>0,a≠1,且x>y>0,N∈N,则下列八个等式: ①(logax)n=nlogx; ②(logax)n=loga(xn); ③-logax=loga( 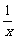 ); );④ 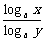 =loga( =loga(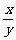 ); );⑤ 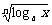 = =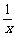 logax; logax;⑥ 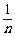 logax=loga logax=loga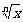 ; ;⑦an 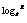 =xn; =xn;⑧loga 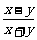 =-loga =-loga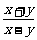 .其中成立的有________个. .其中成立的有________个. |
学生思考,口答,教师板演、点评. 例1分析:利用对数运算性质直接化简. (1) (2) = 小结:此题关键是要记住对数运算性质的形式,要求学生不要记住公式. 例2解(1) (2) 例3(1)解法一: lg14-2lg+lg7-lg18 =lg(2×7)-2(lg7-lg3)+lg7-lg(32×2) =lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0. 解法二:lg14-2lg+lg7-lg18=lg14-lg()2+lg7-lg18=lg=lg1=0. (2)解: ===. (3)解: = ==. 小结:以上各题的解答,体现对数运算法则的综合运用,应注意掌握变形技巧,每题的各部分变形要化到最简形式,同时注意分子、分母的联系,要避免错用对数运算性质. 课本P79练习第1,2,3. 答案:1.(1)lg(xyz)=lgx+lgy+lgz; (2)lg=lg(xy2)-lgz =lgx+lgy2-lgz =lgx+2lgy-lgz; (3)lg 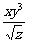 =lg(xy3)-lg 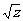 =lgx+lgy3- 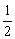 lgz lgz=lgx+3lgy- 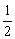 lgz; lgz;(4)lg 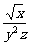 =lg 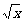 -lg(y2z) -lg(y2z)= 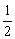 lgx-lgy2-lgz lgx-lgy2-lgz= 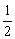 lgx-2lgy-lgz. lgx-2lgy-lgz.2.(1)7;(2)4;(3)-5;(4)0.56. 3.(1)log26-log23 =log2 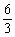 =log22=1; =log22=1;(2)lg5-lg2=lg 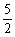 ; ;(3)log53+log5 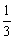 =log53× 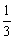 =log51=0; =log51=0;(4)log35-log315 =log3 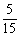 =log3 =log3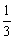 =log33-1 =log33-1=-1. 补充练习答案:4 |
通过例题的解答,巩固所学的对数运算法则,提高运算能力. |
||||||||||||
|
归纳 总结 |
1.对数的运算性质. 2.对数运算法则的综合运用,应掌握变形技巧: (1)各部分变形要化到最简形式,同时注意分子、分母的联系; (2)要避免错用对数运算性质. 3.对数和指数形式比较:
|
学生先自回顾反思,教师点评完善. |
通过师生的合作总结,使学生对本节课所学知识的结构有一个明晰的认识,形成知识体系. |
||||||||||||
|
课后 作业 |
作业:2.1 第四课时 习案 |
学生独立完成 |
巩固新知 提升能力 |
备选例题
例1 计算下列各式的值:
(1)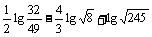 ;
;
(2)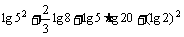 .
.
[解析](1)方法一:
原式=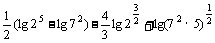
=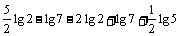
=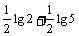
=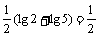 .
.
方法二:原式=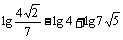
=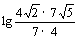
=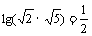 .
.
(2)原式=2lg5 + 2lg2 + lg5 (2lg2 + lg5) + (lg2)2
=2lg10 + (lg5 + lg2)2
= 2 + (lg10)2
= 2 + 1 = 3.
[小结]易犯lg52 = (lg5)2的错误.
这类问题一般有两种处理方法:一种是将式中真数的积、商、方根运用对数的运算法则将它们化为对数的和、差、积、商,然后化简求值;
另一种方法是将式中的对数的和、差、积、商运用对数的运算法则将它们化为真数的积、商、幂、方根,然后化简求值. 计算对数的值时常用到lg2 + lg5 = lg10 = 1.
例2:(1)已知lg2 = 0.3010,lg3 = 0.4771,求lg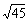 ;
;
(2)设logax = m,logay = n,用m、n表示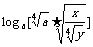 ;
;
(3)已知lgx = 2lga + 3lgb – 5lgc,求x.
[分析]由已知式与未知式底数相同,实现由已知到未知,只须将未知的真数用已知的真数的乘、除、幂表示,借助对数运算法则即可解答.
[解析](1)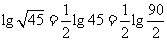


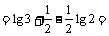 0.4771+0.5 –
0.1505
0.4771+0.5 –
0.1505
= 0.8266
(2)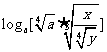

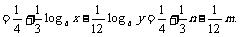
(3)由已知得:
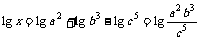 ,
,
∴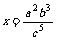 .
.
[小结]①比较已知和未知式的真数,并将未知式中的真数用已知式的真数的乘、除、乘方表示是解题的关键,并且应注意对数运算法则也是可逆的;②第(3)小题利用下列结论:同底的对数相等,则真数相等. 即logaN = logaM N = M.
N = M.
针对本节课公式多、思维量大的特点,采取实例归纳,诱思探究,引导发现等方法.
2.教学难点: 对数的运算性质发现过程及其证明.
1.教学重点:对数运算性质及其推导过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com