
22.本小题主要考查函数的单调性、极值、导数、不等式等基本知识,考查运用导数研究函数性质的方法,考查分类讨论、化归以及数形结合等数学思想方法,考查分析问题、解决问题的能力.满分14分.
解:(Ⅰ)由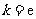 得
得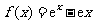 ,所以
,所以 .
.
由 得
得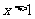 ,故
,故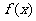 的单调递增区间是
的单调递增区间是 ,
,
由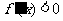 得
得 ,故
,故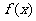 的单调递减区间是
的单调递减区间是 .
.
(Ⅱ)由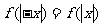 可知
可知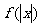 是偶函数.
是偶函数.
于是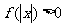 对任意
对任意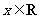 成立等价于
成立等价于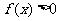 对任意
对任意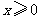 成立.
成立.
由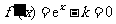 得
得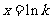 .
.
①当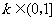 时,
时, .
.
此时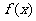 在
在 上单调递增.
上单调递增.
故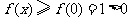 ,符合题意.
,符合题意.
②当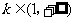 时,
时,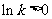 .
.
当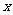 变化时
变化时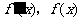 的变化情况如下表:
的变化情况如下表:
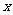 |
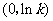 |
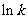 |
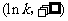 |
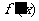 |
 |
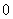 |
 |
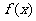 |
单调递减 |
极小值 |
单调递增 |
由此可得,在 上,
上,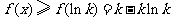 .
.
依题意,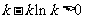 ,又
,又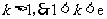 .
.
综合①,②得,实数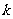 的取值范围是
的取值范围是 .
.
(Ⅲ)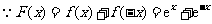 ,
,

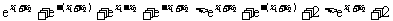 ,
,
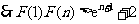 ,
,
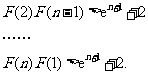
由此得,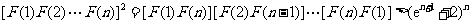
故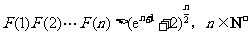 .
.
数学科学段测试(导数部分)
21. 本小题主要考查函数导数的概念与计算,利用导数研究函数的单调性、极值和证明不等式的方法,考查综合运用有关知识解决问题的能力.本小题满分14分.
(Ⅰ)解:根据求导法则有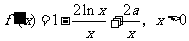 ,
,
故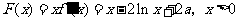 ,
,
于是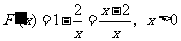 ,
,
列表如下:
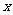 |
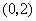 |
2 |
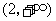 |
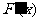 |
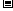 |
0 |
 |
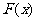 |
 |
极小值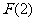 |
 |
故知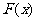 在
在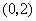 内是减函数,在
内是减函数,在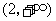 内是增函数,所以,在
内是增函数,所以,在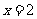 处取得极小值
处取得极小值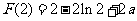 .
.
(Ⅱ)证明:由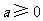 知,
知,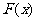 的极小值
的极小值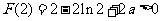 .
.
于是由上表知,对一切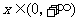 ,恒有
,恒有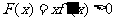 .
.
从而当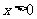 时,恒有
时,恒有 ,故
,故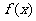 在
在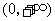 内单调增加.
内单调增加.
所以当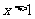 时,
时,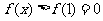 ,即
,即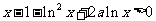 .
.
故当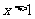 时,恒有
时,恒有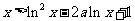 .
.
20.解:⑴∵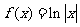 ,
,
∴当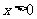 时,
时,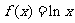 ; 当
; 当 时,
时,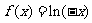
∴当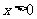 时,
时,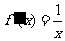 ; 当
; 当 时,
时,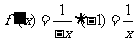 .
.
∴当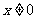 时,函数
时,函数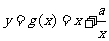 .
.
⑵∵由⑴知当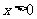 时,
时,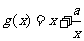 ,
,
∴当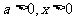 时,
时,  当且仅当
当且仅当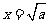 时取等号.
时取等号.
∴函数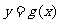 在
在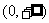 上的最小值是
上的最小值是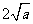 ,∴依题意得
,∴依题意得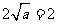 ∴
∴ .
.
⑶由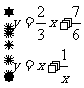 解得
解得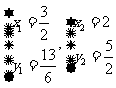
∴直线 与函数
与函数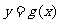 的图象所围成图形的面积
的图象所围成图形的面积
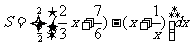 =
=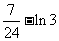
19. 解: 答f(x)在[-4,4]上是单调递减函数.
证明:∵函数f(x)的图象关于原点成中心对称,
则f(x)是奇函数,所以a=1,b=0,于是f(x)=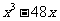
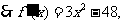 ∴当
∴当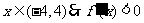
又∵函数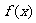 在
在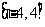 上连续
上连续
所以f(x)在[-4,4]上是单调递减函数.
18.解:⑴由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为 (-1,-4).
⑵∵直线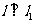 ,
,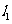 的斜率为4,∴直线l的斜率为
的斜率为4,∴直线l的斜率为 ,
,
∵l过切点P0,点P0的坐标为 (-1,-4)
∴直线l的方程为 即
即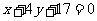 .
.
17.解:∵当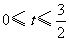 时,
时,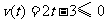 ; 当
; 当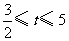 时,
时,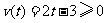 .
.
∴物体从时刻t=0秒至时刻 t=5秒间运动的路程
 =
=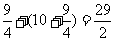 (米)
(米)
15. 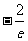 (或
(或 ) 16、
) 16、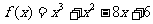
13. 2 14.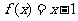
1-5:ABCAD 6-10:BCD B B 11-12:C B
22.(本小题满分14分)
已知函数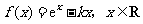
(Ⅰ)若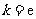 ,试确定函数
,试确定函数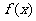 的单调区间;
的单调区间;
(Ⅱ)若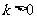 ,且对于任意
,且对于任意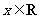 ,
,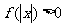 恒成立,试确定实数
恒成立,试确定实数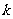 的取值范围;
的取值范围;
(Ⅲ)设函数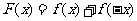 ,求证:
,求证: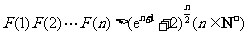 .
.
《导数及其应用》章节测试题答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com