
表1所示为某地区农事活动安排。根据表中提供的信息回答4-6题。
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
农事活动 |
|
|
施肥 |
种植玉米和大豆 |
田间作物管理和除草 |
收割 |
翻土 |
4.依表1所显示的信息可知,该地区应位于( )
A.密西西比平原 B.湄公河三角洲 C.拉普拉塔平原 D.亚马孙平原
5.当地球绕太阳公转到远日点时,该地区农事安排有可能为( )
A.种植大豆 B.收割玉米 C.田间除草 D.犁地翻土
6.考虑耕种作物的特点,在该地田间基本上不需要施加的肥料是( )
A.有机肥 B.磷肥 C.钾肥 D.氮肥
图1所显示的是我国某地形区。读图完成1-3题。
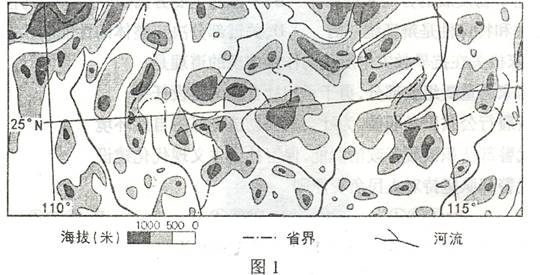
1.分布在图示地区较为普遍的景观是( )
A.黄土 窑洞 B.稻田 茶园 C.绿洲 牧场 D.长城 沙滩
2.该地形区的南、北分别为( )
A.黄河流域 海河流域 B.长江流域 黄河流域
C.长江流域 淮河流域 D.珠江流域 长江流域
3.为更好地监测该地形区地表环境的动态变化应采用( )
A.地理信息系统 B.抽样调查 C.全球定位系统 D.遥感技术
(17)(本小题满分10分)
已知数列 的前
的前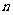 项和为
项和为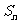 ,
,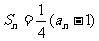
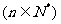
(Ⅰ)求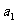 ,
,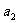 ;
;
(Ⅱ)求数列 的通项公式。
的通项公式。
(18)(本小题满分10分)
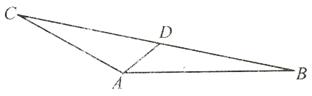
在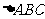 中,
中,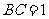 ,
,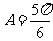 ,
, 是
是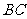 的中点,将
的中点,将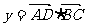 表示为角
表示为角 的函数,并求这个函数的值域.
的函数,并求这个函数的值域.
(19)(本小题满分12分)
商家对某种商品进行促销活动,顾客每购买一件该商品就即刻抽奖,奖励额度如下:
|
奖励等级 |
一等奖 |
二等奖 |
|
所占比例 |
10% |
30% |
|
奖金数(元) |
100 |
20 |
一顾客购买该商品2件,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得奖金数不小于100元的概率.
(20)(本小题满分12分)
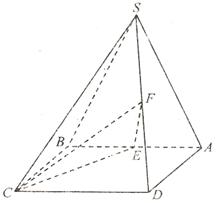 如图,四棱锥
如图,四棱锥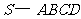 的底面
的底面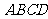 是正方形,侧面
是正方形,侧面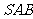 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面,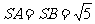 ,
,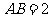 ,
,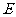 、
、 分别是
分别是 、
、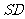 的中点。
的中点。
(Ⅰ)求证: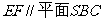 ;
;
(Ⅱ)求二面角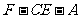 的大小。
的大小。
(21)(本小题满分12分)
已知函数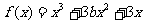 有极值点.
有极值点.
(Ⅰ)求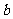 的取值范围;
的取值范围;
(Ⅱ)若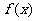 有两个极值点
有两个极值点 、
、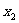 ,且
,且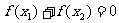 ,求
,求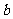 的值。
的值。
(22)(本小题满分12分)
设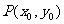 是双曲线
是双曲线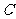 :
: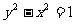 上一点,直线
上一点,直线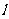 方程是
方程是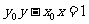
(Ⅰ)判断直线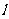 与双曲线
与双曲线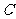 有几个公共点?并说明理由;
有几个公共点?并说明理由;
(Ⅱ)若直线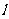 与双曲线
与双曲线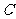 的两条渐近线分别相交于
的两条渐近线分别相交于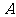 、
、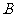 两点,求证
两点,求证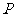 为线段
为线段 的中点.
的中点.
唐山市2008~2009学年度高三年级第一次模拟考试
(13)从含有50个个体的总体中一次性地抽取5个个体,假定其中每个个体被抽取的概率相等,则个体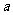 被抽到的概率等于 。
被抽到的概率等于 。
(14)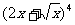 的展开式中
的展开式中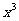 的系数是
.(用数字作答)
的系数是
.(用数字作答)
(15)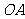 、
、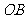 (
(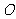 为原点)是圆
为原点)是圆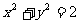 的两条互相垂直的半径,
的两条互相垂直的半径,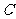 是该圆上任一点,且
是该圆上任一点,且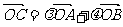 ,则
,则 .
.
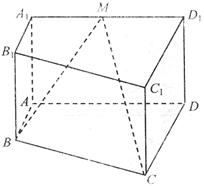 (16)如图,直四棱柱
(16)如图,直四棱柱 的底面是直角梯形,
的底面是直角梯形, ,
, ,
,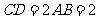 ,
,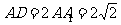 ,
,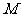 是
是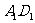 的中点,则
的中点,则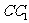 与面
与面 所成角的大小为 .
所成角的大小为 .
(1)等差数列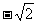 ,
,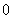 ,
, ,…的第15项为( )
,…的第15项为( )
(A)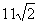 (B)
(B)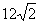 (C)
(C)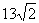 (D)
(D)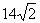
(2)已知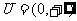 ,
,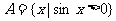 ,
,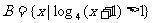 ,则
,则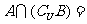 ( )
( )
(A)  (B)
(B) 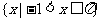
(C) 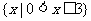 (D)
(D) 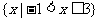
(3)球的一个截面是半径为3的圆,球心到这个截面的距离是4,则该球的表面积是( )
(A) (B)
(B)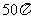 (C)
(C) 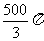 (D)
(D) 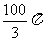
(4)圆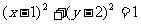 与圆
与圆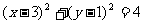 的公切线共有( )
的公切线共有( )
(A)1条 (B)2条 (C)3条 (D)4条
(5)已知实数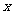 ,
, 满足不等式组
满足不等式组 ,则
,则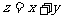 的取值范围是( )
的取值范围是( )
(A)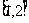 (B)
(B)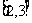 (C)
(C) 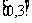 (D)
(D) 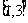
(6)函数
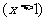 的反函数为( )
的反函数为( )
(A)
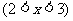 (B)
(B) 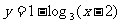
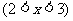
(C) 
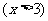 (D)
(D)
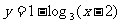
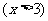
(7)已知椭圆的中心在原点,离心率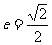 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线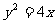 的焦点重合,则此椭圆方程为( )
的焦点重合,则此椭圆方程为( )
(A)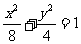 (B)
(B) 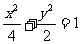 (C)
(C) 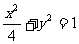 (D)
(D) 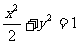
(8)若函数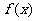 的部分图象如图所示,则该函数可能是( )
的部分图象如图所示,则该函数可能是( )
(A)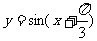 (B)
(B) 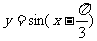
(C) 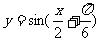 (D)
(D) 
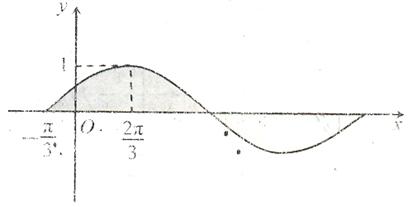
(9)设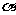 、
、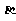 、
、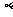 为三个不同的平面,
为三个不同的平面,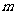 、
、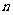 为两条不同的直线,在
为两条不同的直线,在
①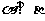 ,
, ,
,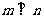 ; ②
; ②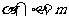 ,
,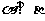 ,
,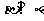 ;
;
③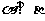 ,
,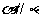 ,
,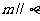 ; ④
; ④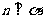 ,
,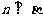 ,
,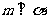
中,是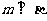 的充分条件的为( )
的充分条件的为( )
(A) ①② (B)②④ (C)②③ (D) ③④
(10)已知函数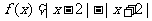 ,则使得
,则使得 的
的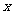 的取值范围是( )
的取值范围是( )
(A) 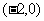 (B)
(B) 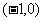 (C)
(C) 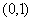 (D)
(D) 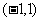
(11)已知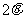 是第一象限的角,且
是第一象限的角,且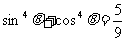 ,那么
,那么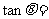 ( )
( )
(A) 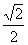 (B)
(B) 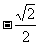 (C)
(C) 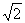 (D)
(D) 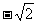
(10)从5种不同的水果和4种不同的糖果中各选出3种,放入如图所示的6个不同区域(用数字表示)中拼盘,每个区域只放一种,且水果不能放在有公共边的相邻区域内,则不同的放法有( )
(A) 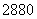 种 (B)
种 (B) 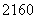 种 (C)
种 (C) 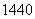 种 (D)
种 (D) 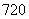 种
种

参考公式:
如果事件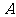 、
、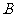 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式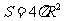
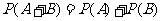 其中
其中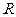 表示球的半径
表示球的半径
如果事件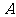 、
、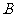 相互独立,那么
球的体积公式
相互独立,那么
球的体积公式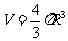
 其中
其中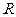 表示球的半径
表示球的半径
如果事件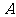 在一次试验中发生的概率是
在一次试验中发生的概率是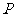 ,
,
那么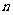 次独立重复试验中恰好发生
次独立重复试验中恰好发生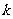 次的概率:
次的概率:
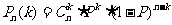
20、定义在定义域D内的函数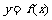 ,若对任意的
,若对任意的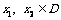 都有
都有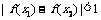 ,
,
则称函数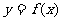 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数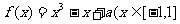 ,
,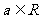 )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
19、 请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点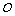 到底面中心
到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
[注: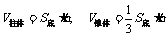 ]
]
18、已知 在时有极值0。
在时有极值0。
(1)求常数
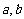 的值; (2)求的单调区间。
的值; (2)求的单调区间。
(3)方程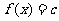 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数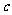 的范围。
的范围。
17、[理]已知一物体运动的速度为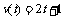 ,求物体在
,求物体在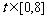 内运动的路程。
内运动的路程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com