3、磁极：磁体的各部分磁性强弱不同，磁性最强的区域叫磁极(S极和N极)。

2、磁体：具有磁性的物体叫磁体。

1、磁性：物质具有吸引铁质物体的性质叫做磁性。

2、在水平面内作圆周运动的临界问题

在水平面上做圆周运动的物体，当角速度ω变化时，物体有远离或向着圆心运动的(半径有变化)趋势。这时，要根据物体的受力情况，判断物体受某个力是否存在以及这个力存在时方向朝哪(特别是一些接触力，如静摩擦力、绳的拉力等)。

1、在竖直平面内作圆周运动的临界问题

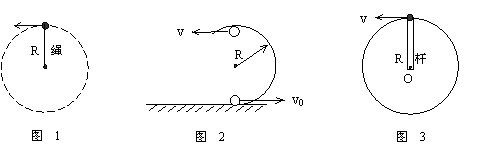
⑴如图1、图2所示，没有物体支承的小球，在竖直平面作圆周运动过最高点的情况

①临界条件：绳子或轨道对小球没有力的作用

　　　　v_临界＝

②能过最高点的条件：v≥，当v＞时，绳对球产生拉力，轨道对球产生压力。

③不能过最高点的条件：v＜v_临界(实际上球没到最高点时就脱离了轨道)。

⑵如图3所示情形，小球与轻质杆相连。杆与绳不同，它既能产生拉力，也能产生压力

①能过最高点v临界＝0，此时支持力N＝mg

②当0＜v＜时，N为支持力，有0＜N＜mg，且N随v的增大而减小

③当v＝时，N＝0

④当v＞，N为拉力，有N＞0，N随v的增大而增大

4．实例：典型的非匀速圆周运动是竖直面内的圆周运动

(1)如图4-3-1和4-3-2所示，没有物体支撑的小球，在竖直面内作圆周运动通过最高点

①临界条件是绳子或轨道对小球没有力的作用，在最高点v=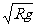．②小球能通过最高点的条件是在最高点v>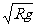．③小球不能通过最高点的条件是在最高点v<．

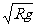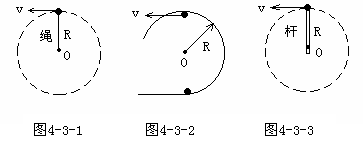
(2)如图4-3-3所示，球过最高点时，轻质杆对小球的弹力情况是①小球在最高点v=0时，是支持力．②小球在最高点0<v<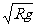时，是支持力．③小球在最高点v=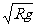时，作用力为零．④小球在最高点v>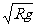时，是拉力．

3．处理圆周运动动力学问题般步骤

(1)确定研究对象，进行受力分析，画出运动草图

(2)标出已知量和需求的物理量

(3)建立坐标系，通常选取质点所在位置为坐标原点，其中一条轴与半径重合

(4)用牛顿第二定律和平衡条件建立方程求解．

2．遵守的动力学规律

(1)向心加速度：a=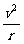或a=ω²r

(2)力和运动的关系：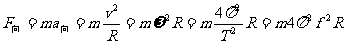

1．变速圆周运动特点：

(1)速度大小变化--有切向加速度、速度方向改变--有向心加速度．

故合加速度不一定指向圆心．

(2)合外力不全部提供作为向心力，合外力不指向圆心．

5．向心加速度：它是沿着半径指向圆心的加速度，是描述线速度方向改变快慢的物理量，它的大小与线速度、角速度的关系是a=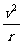=ω²r．