
5.(07江西)若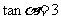 ,
,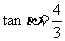 ,则
,则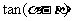 等于
等于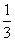
4.(07江西)若 ,则
,则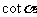 等于
等于
3.(07福建)sin15°cos75°+cos15°sin105°等于1
2.(07天津) 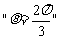 是
是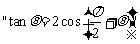 的充分而不必要条件
的充分而不必要条件
公式组一

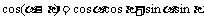

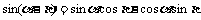
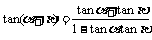
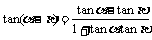
公式组二: 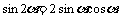
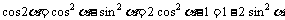
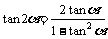
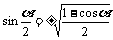
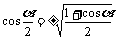 ,
,
公式组三
 ,
,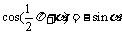
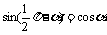
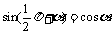 ,
,
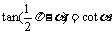 ,
,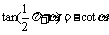
常用数据: 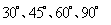 的三角函数值
的三角函数值
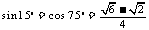 ,
,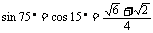
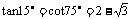 ,
,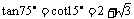
注: ⑴以上公式务必要知道其推导思路,从而清晰地“看出”它们之间的联系,它们的变化形式.如
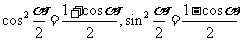 等.
等.
从而可做到:正用、逆用、变形用自如使用各公式.
⑵三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备.
⑶三角函数恒等变形的基本策略。
①常值代换:特别是用“1”的代换,如1=cos2θ+sin2θ=tanx·cotx=tan45°等。
②项的分拆与角的配凑。如分拆项: ;
;
配凑角(常用角变换):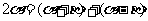 、
、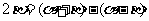 、
、
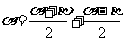 、
、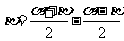 、
、 等.
等.
③降次与升次。即倍角公式降次与半角公式升次。
④化弦(切)法。将三角函数利用同角三角函数基本关系化成弦(切)。
⑤引入辅助角。asinθ+bcosθ=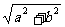 sin(θ+
sin(θ+ ),这里辅助角
),这里辅助角 所在象限由a、b的符号确定,
所在象限由a、b的符号确定, 角的值由tan
角的值由tan =
= 确定。
确定。
典型例题
例1、同角三角函数的基本关系
已知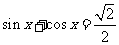 ,求
,求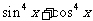 .
.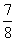
变式1:已知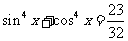 ,
,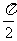 <x<
<x< ,求
,求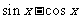 的值.1/2
的值.1/2
变式2、化简: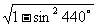 sin10
sin10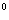
例2、两角和与差及二倍角的三角函数
已知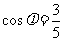 ,
,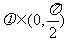 ,求
,求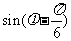 ,
, 的值.
的值.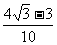 ,-7
,-7
变式1.已知tanα,tanβ是方程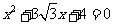 两根,且α,β
两根,且α,β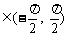 ,则α+β等于
,则α+β等于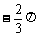 或
或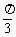 变式2.
变式2.  的值是4
的值是4
变式3. 设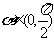 ,若
,若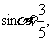 则
则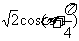 =
=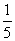
变式4.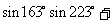

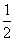
变式5:在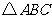 中,已知
中,已知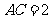 ,
,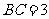 ,
,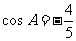 .
.
(Ⅰ)求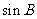 的值;
的值; 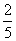
(Ⅱ)求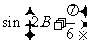 的值.
的值.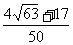
变式6:在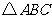 中,
中,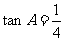 ,
,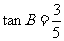 .
.
(Ⅰ)求角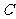 的大小;135
的大小;135
(Ⅱ)若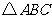 最大边的边长为
最大边的边长为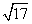 ,求最小边的边长.
,求最小边的边长.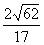
变式7:已知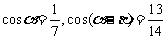 ,且
,且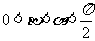 ,
,
(Ⅰ)求 的值;-
的值;-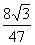
(Ⅱ)求 .
.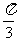
实战训练
1.(07全国)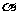 是第四象限角,
是第四象限角, ,则
,则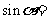

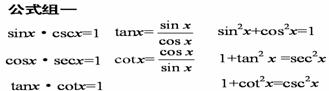
公式组二 (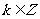 )
)
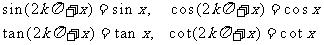
公式组三
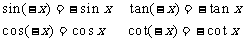
公式组四 公式组五

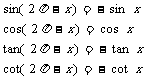
公式组六
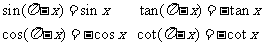
21.若关于x的方程2cos2(p + x) - sinx + a = 0 有实根,求实数a的取值范围
20. 在△ABC中,已知cosA =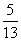 ,sinB =
,sinB =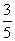 ,则cosC的值为
,则cosC的值为
19. 已知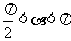 ,
,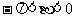 ,tana =
,tana =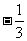 ,tanb =
,tanb =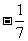 ,求2a + b.
,求2a + b.
18.已知锐角a,b满足cosa=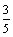 ,cos(a+b)=
,cos(a+b)=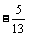 ,求cosb.
,求cosb.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com