6．(2007年江西卷文2)．函数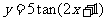的最小正周期为　　　　

5．(2007年辽宁卷7)．若函数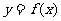的图象按向量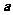平移后，得到函数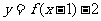的图象，则向量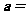　　　　　

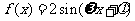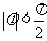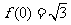4．(07年浙江卷理2)若函数，(其中，)的最小正周期是，且，则　　　　　　

3．函数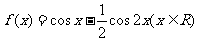的最大值等于　　　

2. 函数的最小正周期是____

1．函数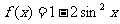的最小正周期为　　　

9．已知f(x)=5sinxcosx-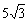cos²x+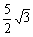(x∈R)

⑴求f(x)的最小正周期；

⑵求f(x)单调区间；

⑶求f(x)图象的对称轴，

典型例题

例1、三角函数图像变换

将函数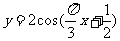的图像作怎样的变换可以得到函数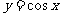的图像？

变式1：将函数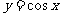的图像作怎样的变换可以得到函数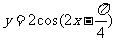的图像？

例2、已知简谐运动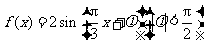的图象经过点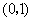，则该简谐运动的最

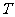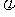小正周期和初相分别为　　　　　　　　

例3、三角函数性质

求函数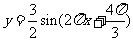的最大、最小值以及达到最大(小)值时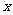的值的集合

变式1：函数y=2^sinx的单调增区间是　　　　　　　　　　　　　　　

变式2、下列函数中，既是(0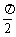，)上的增函数，又是以π为周期的偶函数是( )

(A)y=lgx²　　　　 　　 　(B)y=|sinx|　　　 　　 　(C)y=cosx　　　 (D)y=

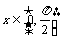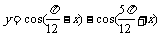变式3、已知，求函数的值域

变式4、已知函数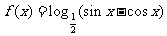　

⑴求它的定义域和值域；　　　

⑵求它的单调区间；

⑶判断它的奇偶性；　　　　　

⑷判断它的周期性.

例4、三角函数的简单应用

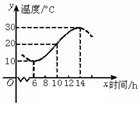如图，某地一天从6时至14时的温度变化曲线近似

满足函数y=Asin(ωx+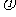)+b.

(Ⅰ)求这段时间的最大温差；

(Ⅱ)写出这段曲线的函数解析式．

例5、三角恒等变换

函数y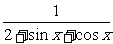＝的最大值是　　　　　　　 ．

变式1：已知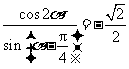，求的值．

变式2：已知函数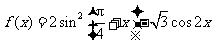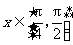，．求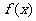的最大值和最小值．

实战训练

8． 函数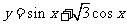在区间[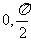]的最小值为______.

7．将函数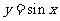的图象上各点的横坐标扩大为原来的2倍，纵坐标不变，再把所得图象上所有点向左平移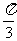个单位，所得图象的解析式是　　　　 　　　.

6．为了得到函数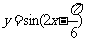的图象，可以将函数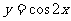的图象向　 平移　 个单位长度