
1、 能够讲出函数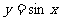 的图象和函数
的图象和函数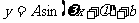 的图象之间的平移伸缩变换关系.
的图象之间的平移伸缩变换关系.
2、 能够对照图象讲出正切函数的相关性质:定义域、值域、对称中心、奇偶性、单调性、周期性.
§1.5、函数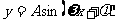 的图象
的图象
1、记住正切函数的图象:
1、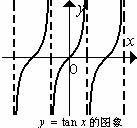 周期函数定义:对于函数
周期函数定义:对于函数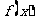 ,如果存在一个非零常数T,使得当
,如果存在一个非零常数T,使得当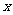 取定义域内的每一个值时,都有
取定义域内的每一个值时,都有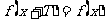 ,那么函数
,那么函数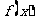 就叫做周期函数,非零常数T叫做这个函数的周期.
就叫做周期函数,非零常数T叫做这个函数的周期.
§1.4.3、正切函数的图象与性质
3、 会用五点法作图.
§1.4.2、正弦、余弦函数的性质
2、 能够对照图象讲出正弦、余弦函数的相关性质:定义域、值域、最大最小值、对称轴、对称中心、奇偶性、单调性、周期性.
1、记住正弦、余弦函数图象:
5、诱导公式六: 
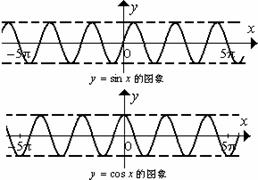 §1.4.1、正弦、余弦函数的图象
§1.4.1、正弦、余弦函数的图象
4、诱导公式五: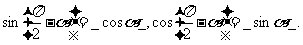
3、诱导公式四: 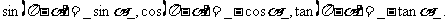
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com