
(一)习题讲解:《习案》P173面6题。
(六)作业:《习案》作业二十七。
第二章 平面向量复习课(二)
(五)、小结:掌握向量的相关知识。
(四)基础练习:
《习案》P178面6题、P180面3题。
(三)典型例题
例1. 已知O为△ABC内部一点,∠AOB=150°,∠BOC=90°,设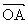 =
=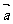 ,
,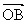 =
=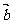 ,
,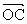 =
=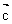 ,
,
且|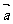 |=2,|
|=2,|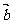 |=1,|
|=1,| 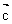 |=3,用
|=3,用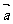 与
与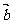 表示
表示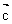
解:如图建立平面直角坐标系xoy,其中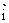 ,
,  是单位正交基底向量, 则B(0,1),C(-3,0),
是单位正交基底向量, 则B(0,1),C(-3,0),
设A(x,y),则条件知x=2cos(150°-90°),y=-2sin(150°-90°),即A(1,-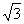 ),也就是
),也就是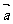 =
=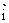 -
-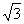
 ,
, 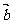 =
= ,
, 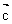 =-3
=-3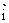 所以-3
所以-3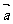 =3
=3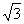
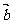 +
+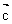 |即
|即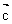 =3
=3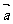 -3
-3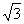
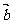
(二)习题讲解:《习案》P167 面2题,P168面6题,P169面1题,P170面5、6题,
P171面1、2、3题,P172面5题,P173面6题。
(一)重点知识:
1. 实数与向量的积的运算律:
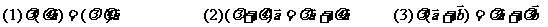

2. 平面向量数量积的运算律:
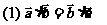
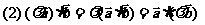
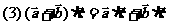

3. 向量运算及平行与垂直的判定:
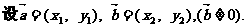

则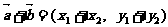
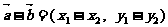
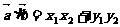

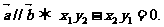
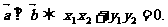

4. 两点间的距离: 
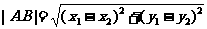

5. 夹角公式:
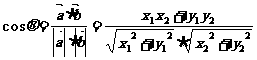

6. 求模:
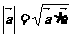
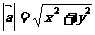
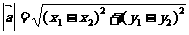
向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体,能与中学数学教学内容的许多主干知识综合,形成知识交汇点,所以高考中应引起足够的重视. 数量积的主要应用:①求模长;②求夹角;③判垂直
8. 数量积(点乘或内积)的概念,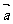 ·
·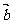 =|
=|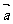 ||
||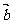 |cos
|cos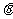 =x
=x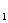 x
x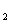 +y
+y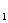 y
y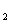 注意区别“实数与向量的乘法;向量与向量的乘法”
注意区别“实数与向量的乘法;向量与向量的乘法”
7. 向量的坐标运算(加.减.实数和向量的乘法.数量积)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com