
7.射影及有关性质
(1)点在平面上的射影自一点向平面引垂线,垂足叫做这点在这个平面上的射影,点的射影还是点.
(2)直线在平面上的射影自直线上的两个点向平面引垂线,过两垂足的直线叫做直线在这平面上的射影.
(4)射影的有关性质
从平面外一点向这个平面所引的垂线段和斜线段中:
(i)射影相等的两条斜线段相等,射影较长的斜线段也较长;
(ii)相等的斜线段的射影相等,较长的斜线段的射影也较长;
(iii)垂线段比任何一条斜线段都短.
6.线面平行与垂直的判定
(1)两直线平行的判定
①定义: .
②判定定理 ,即若a∥α,a?β,α∩β=b,则a∥b.
③公理4 ,即若a∥b,b∥c,则a∥c.
④线面垂直的性质定理 ,即若a⊥α,b⊥α,则a∥b
⑤面面平行的性质定理 ,即若α∥β,α∩γ,β∩γ=b,则a∥b
(2)两直线垂直的判定
①定义: .
②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c
③线面垂直的定义
.即若a⊥α,b α,a⊥b.④三垂线定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.
α,a⊥b.④三垂线定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.
(3)直线与平面平行的判定
①定义: .
②判定定理
.即若a α,b
α,b α,a∥b,则a∥α.
α,a∥b,则a∥α.
③面面平行的定义
,即若α∥β,l α,则l∥β.
α,则l∥β.
(4)直线与平面垂直的判定
①定义: .
②线面垂直的判定
.即若m α,n
α,n α,m∩n=B,l⊥m,l⊥n,则l⊥α.
α,m∩n=B,l⊥m,l⊥n,则l⊥α.
③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.
④面面平行的性质 ,即若α∥β,l⊥β,则l⊥α.
(5)两平面平行的判定
①定义:
,即无公共点 α∥β.
α∥β.
②面面平行的判定
,即若a,b α,a∩b=P,a∥β,b∥β,则α∥β.
α,a∩b=P,a∥β,b∥β,则α∥β.
③ .即若α⊥a,β⊥a,则α∥β.
④ .即若α∥β,β∥γ,则α∥γ.
(6)两平面垂直的判定
①定义:
,即二面角α-a-β=90° α⊥β.
α⊥β.
②面面垂直的判定
,即若l⊥β,l α,则α⊥β.
α,则α⊥β.
③ .即若α∥β,α⊥γ,则β⊥γ.
(7)线、线关系和线、面关系的辨证法


5.异面直线的判定
证明两条直线是异面直线通常采用反证法.
有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.
4.空间线面的位置关系
 平行-没有公共点
平行-没有公共点
共面
(1)直线与直线 相交-有且只有一个公共点
异面(既不平行,又不相交)
 直线在平面内-有无数个公共点
直线在平面内-有无数个公共点
 (2)直线和平面 直线不在平面内 平行-没有公共点
(2)直线和平面 直线不在平面内 平行-没有公共点
(直线在平面外) 相交-有且只有一个公共点
 相交-有一条公共直线(无数个公共点)
相交-有一条公共直线(无数个公共点)
(3)平面与平面
平行-没有公共点
2.平面的基本性质
公理1 _________________________________________________________________.
公理2 __________________________________________________________________.
公理3 _______________________________________________________________.
推论1___________________________________________________________________.
推论2 ___________________________________________________________________.
推论3 ___________________________________________________________________
|
 3.证题方法
3.证题方法
|
|
 |
|||
|
|||
|
1、平面:几何里的平面是无限伸展的.平面通常用一个平行四边形来表示.
(1)平面的表示方法: 。
(2)用集合论中的符号表示它们之间的关系,例如:A∈l表示 上;
________表示点A不在平面α内;__________表示直线l在平面α内;
_________表示直线a不在平面α内;l∩m=A表示_____________________;
α∩l=A表示平面_______________;α∩β=l表示_______________________.
16.有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计).有人应用数学知识作如下设计:在钢板的四个角处各切去一个小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长. (1)请你求出这种切割、焊接而成的长方体容器的的最大容积V1; (2)请你判断上述方案是否最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积V2>V1.
15.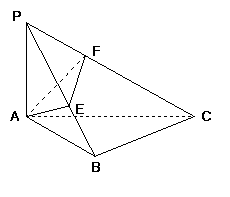 如图,
如图, 为
为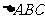 所在平面外一点,
所在平面外一点,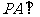 平面
平面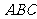 ,
,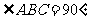 ,
,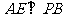 于
于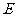 ,
,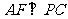 于
于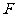 ,求证:(1)
,求证:(1)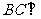 平面
平面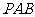 ;(2)
;(2)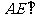 平面
平面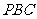 ;(3)
;(3)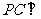 平面
平面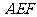 .
.
13.某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD-A1B1C1D1的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA1→A1D1→…,黄“电子狗”爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i是正整数).设黑“电子狗”爬完2006段、黄“电子狗”爬完2005段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是( )
A.0 B.1 C.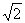 D.
D.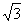
 14如图是一个长方体ABCD-A1B1C1D1截去一个角后的
14如图是一个长方体ABCD-A1B1C1D1截去一个角后的
多面体的三视图,在这个多面体中,AB=4,BC=6,
CC1=3.则这个多面体的体积为 .
12.正四棱柱ABCD–A1B1C1D1中,AB=3,BB1=4.长为1的线段PQ在棱AA1上移动,长为3的线段MN在棱CC1上移动,点R在棱BB1上移动,则四棱锥R–PQMN的体积是( )
A.6 B.10 C.12 D.不确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com