
读经纬网图,回答第1题:

1.图中阴影的面积一样,实际面积大小是:
A.甲等于乙 B.甲小于乙 C.甲大于乙 D.无法确定
20、(Ⅰ)由题意,得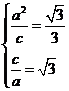 ,解得
,解得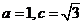 ,
,
∴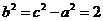 ,∴所求双曲线
,∴所求双曲线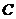 的方程为
的方程为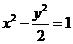 .....4分
.....4分
(Ⅱ)设A、B两点的坐标分别为 ,线段AB的中点为
,线段AB的中点为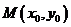 ,
,
由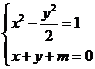 得
得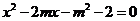 (判别式
(判别式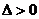 ),
),
∴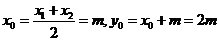 ,
,
∵点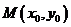 在圆
在圆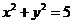 上,∴
上,∴ ,∴
,∴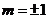
19、(1)380元...........3分;(2)上涨了2元..............7分
(3)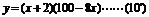 ,即
,即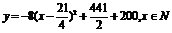
所以x=5时,y取最大值420,即上涨5元可获最大利润420元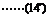
16、解:(1)设甲、乙、丙中奖的事件分别为A、B、C,那么
P(A)=P(B)=P(C)=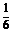
P(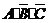 )=P(A)P(
)=P(A)P(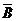 )P(
)P(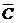 )=
)=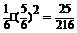
答:甲中奖且乙、丙都没有中奖的概率为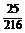 ………………………6分
………………………6分
(2)ξ的可能值为0,1,2,3 P(ξ=k)=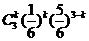 (k=0,1,2,3)
(k=0,1,2,3)
所以中奖人数ξ的分布列为
|
ξ |
0 |
1 |
2 |
3 |


18题、
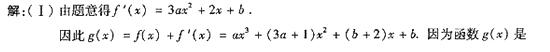

15、
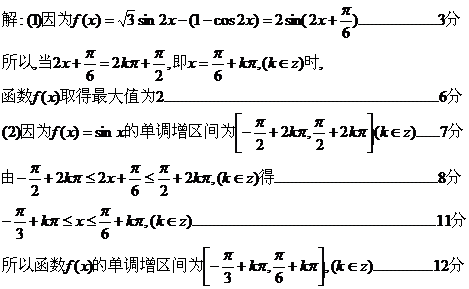
12、b>c>a 13、a=-1,b=2 14、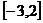
20、(本小题满分14分)
已知双曲线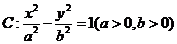 的离心率为
的离心率为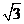 ,右准线方程为
,右准线方程为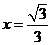 。
。
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线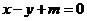 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆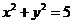 上,求m的值.
上,求m的值.
 [1,2) 10、
[1,2) 10、 11、0
11、0
19、(本题14分)
某公司将进货单价为8元一个的商品按10元一个销售,每天可以卖出100个,若这种商品的销售价每个上涨一元,则销售量就减少8个.
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为336元,那么销售价上涨了几元?
(3)设销售价上涨x元(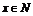 )试将利润y表示为x的函数,并求出上涨几元,可获最大利润.
)试将利润y表示为x的函数,并求出上涨几元,可获最大利润.
18、(本题14分)
已知函数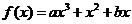 (其中常数a,b∈R),
(其中常数a,b∈R),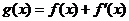 是奇函数.
是奇函数.
(1)求 的表达式;
的表达式;
(2)讨论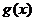 的单调性,并求
的单调性,并求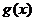 在区间[1,2]上的最大值和最小值.
在区间[1,2]上的最大值和最小值.
17、(本题14分)
如图所示,在长方体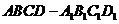 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
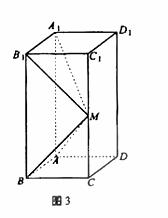 (1)求异面直线A1M和C1D1所成的角的正切值;
(1)求异面直线A1M和C1D1所成的角的正切值;
(2)证明:直线BM⊥平面A1B1M1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com