
3.情态与价值:培养学生通过日常生活中的例子,找到数学知识规率,从而在实际生活问题中数形结合的应用以及计算机在数学中的应用。
2.过程与方法:通过学生对一元二次不等式的解法的理解,利用计算机将数学知识用程序表示出来;
1.知识与技能: 应用一元二次不等式解决日常生活中的实际问题;能用一个程序框图把求解一般一元二次不等式的过程表示出来;
(五)作业:《习案》作业二十三。
(四)小结
1. 从实际问题中建立一元二次不等式,解一元二次不等式;
2.能把一元二次不等式的解的类型归纳出来。
(三)[举例应用]
例1 求下列不等式的解集
(1)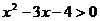 (2)
(2)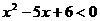
(3)4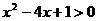 (4)
(4)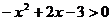
练习:P80面练习1题。
通过以上的例题及练习的讲解,指导学生归纳P77面的表格及一元二次不等式的解的情况。
例2.解不等式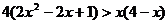
例3.解不等式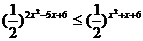
(二)[探索研究]
思考1。一元一次方程、一元一次不等式及与一次函数三者之间有什么关系?
2.不等式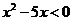 、二次函数
、二次函数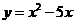 、一元二次方程
、一元二次方程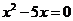 的之间有什么关系?
的之间有什么关系?
容易知道,方程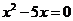 有两个实根:
有两个实根: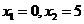 由二次函数的零点与相应的一元二次方程根的关系,知
由二次函数的零点与相应的一元二次方程根的关系,知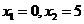 是二次函数
是二次函数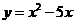 的两个零点。
的两个零点。
通过学生画出的二次函数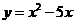 的图象,观察而知,
的图象,观察而知,
当 时,函数图象位于x轴上方,此时
时,函数图象位于x轴上方,此时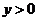 ,即
,即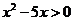 ;
;
当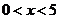 时,函数图象位于x轴下方,此时
时,函数图象位于x轴下方,此时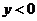 ,即
,即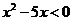 。
。
所以,一元二次不等式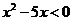 的解集是
的解集是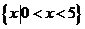 从而解决了以上的上网问题。
从而解决了以上的上网问题。
3.如何解一元二次不等式?
重点:从实际问题中抽象出一元二次不等式模型,围绕一元二次不等式的解法展开,突出体现数形结合的思想;
难点:理解二次函数、一元二次方程与一元二次不等式解集的关系。
3.情态与价值:培养学生通过日常生活中的例子,找到数学知识规率,从而在实际生活问题中数形结合的应用以及计算机在数学中的应用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com