2. 教学难点：两角和与差正弦、余弦和正切公式的灵活运用.

1. 教学重点：两角和、差正弦和正切公式的运用；

2、掌握两角和与差的余弦、正弦和正切公式的应用及类型的变换。

1、理解两角和与差的余弦、正弦和正切公式，体会三角恒等变换特点的过程；

(五)作业：《习案》作业三十。

(四)小结：本节我们学习了两角和与差正弦、余弦和正切公式，我们要熟记公式，学会灵活运用.

(三)例题讲解

例1、已知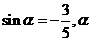是第四象限角，求的值.

解：因为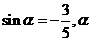是第四象限角，得，

　，

于是有：

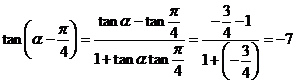
思考：在本题中，，那么对任意角，此等式成立吗？若成立你能否证明？

　 练习：教材P131面1、2、3、4题

例2、已知求的值．()

例3、利用和(差)角公式计算下列各式的值：

(1)、；(2)、；(3)、．

解：(1)、；

(2)、；

(3)、．

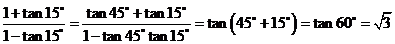练习：教材P131面5题

(二)新课讲授

问题：由两角差的余弦公式，怎样得到两角差的正弦公式呢？

探究1、让学生动手完成两角和与差正弦公式.

．

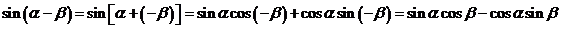
探究2、让学生观察认识两角和与差正弦公式的特征，并思考两角和与差正切公式.(学生动手)

．

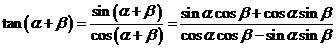探究3、我们能否推倒出两角差的正切公式呢？

探究4、通过什么途径可以把上面的式子化成只含有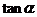、的形式呢？

(分式分子、分母同时除以，得到．

注意：

　　 5、将、、称为和角公式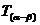，、、称为差角公式。

(一)复习式导入：

(1)大家首先回顾一下两角差的余弦公式：．

　(2)？

2. 教学难点：两角和与差正弦、余弦和正切公式的灵活运用.