
(六)作业:《习案》作业三十二。
(五)小结:本节我们学习了二倍角的正弦、余弦和正切公式,我们要熟记公式,在解题过程中要善于发现规律,学会灵活运用.
(四)练习:教材P135面1、2、3、4、5题
(三)例题讲解
例1、已知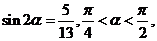 求
求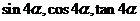 的值.
的值.
解:由 得
得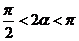 .
.
又因为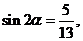
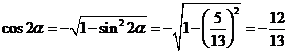 .
.
于是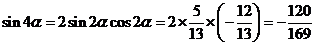 ;
;
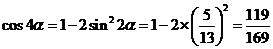 ;
;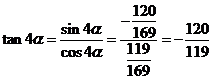 .
.
例2.在△ABC中,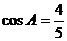 ,
,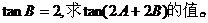
例3.已知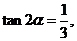 求
求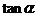 的值.
的值.
解: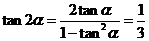 ,由此得
,由此得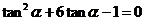
解得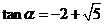 或
或 .
.
例4.已知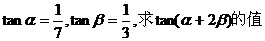
(二)公式推导:
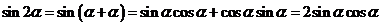 ;
;
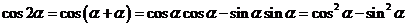 ;
;
思考:把上述关于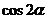 的式子能否变成只含有
的式子能否变成只含有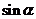 或
或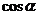 形式的式子呢?
形式的式子呢?
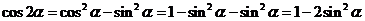 ;
;
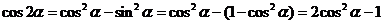 .
.
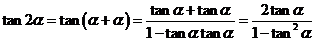 .
.
注意: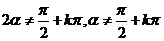
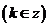
(一)复习式导入:大家首先回顾一下两角和的正弦、余弦和正切公式,
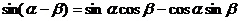


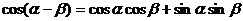
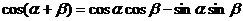

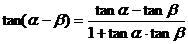
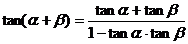

练习:(1)在△ABC中,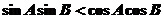 ,则△ABC为( )
,则△ABC为( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.等腰三角形
(2) 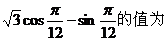 ( )
( )
A. 0 B.2 C.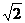 D.
D.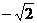
思考:已知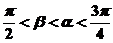 ,
,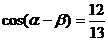 ,
,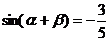 ,求
,求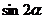
我们由此能否得到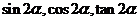 的公式呢?(学生自己动手,把上述公式中
的公式呢?(学生自己动手,把上述公式中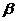 看成
看成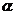 即可),
即可),
教学重点:以两角和的正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式;
教学难点:二倍角的理解及其灵活运用.
以两角和正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式,理解推导过程,掌握其应用.
(二)新课讲授
例1、化简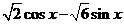
解:此题与我们所学的两角和与差正弦、余弦和正切公式不相象,但我们能否发现规律呢?
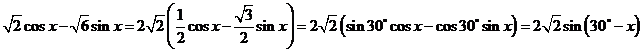 思考:
思考: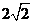 是怎么得到的?
是怎么得到的?
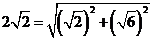 ,我们是构造一个叫使它的正、余弦分别等于
,我们是构造一个叫使它的正、余弦分别等于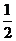 和
和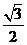 的.
的.
归纳: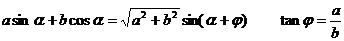
例2、已知:函数
(1)
求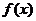 的最值。(2)求
的最值。(2)求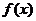 的周期、单调性。
的周期、单调性。
例3.已知A、B、C为△ABC的三內角,向量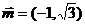 ,
,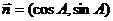 ,且
,且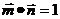 ,
,
(1)
求角A。(2)若 ,求tanC的值。
,求tanC的值。
练习:(1)教材P132面7题
(2)在△ABC中,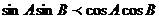 ,则△ABC为( )
,则△ABC为( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.等腰三角形
(2) 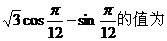 ( )
( )
A. 0 B.2 C.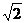 D.
D.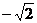
思考:已知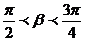 ,
,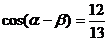 ,
,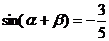 ,求
,求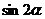
(一)复习式导入:(1)基本公式
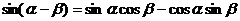
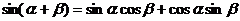

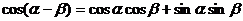
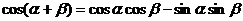

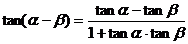
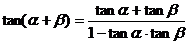

(2)练习:教材P132面第6题。
思考:怎样求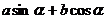 类型?
类型?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com