
20.(天津市六校2010届高三第三次联考文科)(本小题满分12分)
已知数列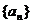 的前n项和为
的前n项和为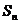 ,且满足
,且满足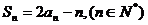
(1)求 的值;
的值;
(2)求数列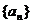 的通项公式;
的通项公式;
(3)若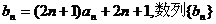 的前n项和为
的前n项和为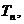 求满足不等式
求满足不等式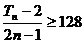 的最小n值.
的最小n值.
21.解:(I)∵点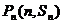 在函数
在函数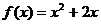 的图像上,
的图像上,
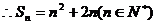 …………2分
…………2分
当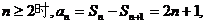
当 满足上式,
满足上式,
所以数列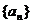 的通项公式为
的通项公式为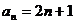 …………4分
…………4分
(II)由 求导得
求导得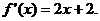
∵在点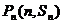 处的切线的斜率为
处的切线的斜率为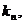
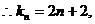 …………5分
…………5分
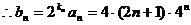
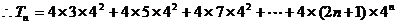
用错位相减法可求得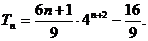 …………9分
…………9分
(III)
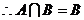
又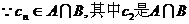 中的最小数,
中的最小数,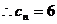
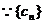 的公差是4的倍数,
的公差是4的倍数,
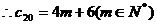 …………11分
…………11分
有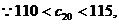
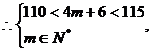 解得m=27.
解得m=27.
所以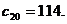
设等差数列的公差为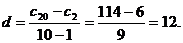
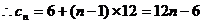 ,即为
,即为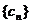 的通项公式 …………14分
的通项公式 …………14分
21.(天津市六校2010届高三第三次联考理科)(本小题14分)
已知数列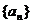 的前n项和为
的前n项和为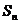 ,对一切正整数n,点
,对一切正整数n,点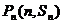 都在函数
都在函数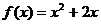 的图像上,且在点
的图像上,且在点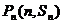 处的切线的斜率为
处的切线的斜率为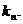
(I)求数列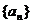 的通项公式;
的通项公式;
(II)若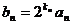 ,求数列
,求数列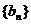 的前n项和
的前n项和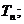
(III)设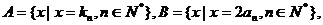 等差数列
等差数列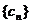 的任一项
的任一项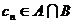 ,其中c1是
,其中c1是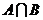 的最小数,
的最小数,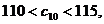 求数列
求数列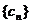 的通项公式.
的通项公式.
22.(天津市武清区2009-2010学年高三下学期第一次模拟文)(本小题满分14分)
已知正项数列{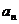 }满足
}满足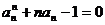 (
(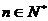 )
)
(1)求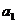 ,
,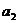 ;
;
(2)求证: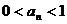
(3)求证: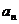 >
>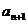 ;
;
(1)∵ 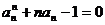 ,
,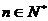
令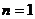 得
得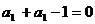 ∴
∴ 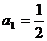 ………………1分
………………1分
令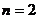 得
得
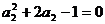 ∴
∴ 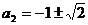
∵ 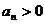 ∴
∴ 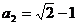 ……………………………3分
……………………………3分
(2)∵ 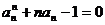 ∴
∴ 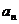 是方程
是方程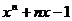 的一个根 ………4分
的一个根 ………4分
设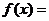
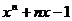 ,则
,则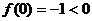 ,
,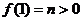 。
。
∴ 方程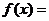 0在(0,1)内至少有一个根。
…………………6分
0在(0,1)内至少有一个根。
…………………6分
∵ 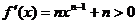 ∴
∴ 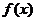 在(0,+∞)上是增函数,…………7分
在(0,+∞)上是增函数,…………7分
∴ 方程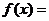 0在(0,+∞)上有唯一的根,且根在(0,1)内,
0在(0,+∞)上有唯一的根,且根在(0,1)内,
∴ 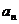 ∈(0,1) ∴
∈(0,1) ∴ 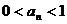 ………………………………9分
………………………………9分
(3)∵ 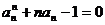 ,∴
,∴
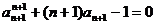
两式相减得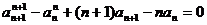 …………………10分
…………………10分
若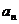 ≤
≤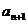 ,∵
,∵
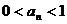 则
则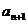 ≥
≥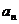 >
>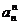 ,
,
从而有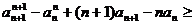
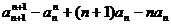
=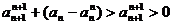 ,
……………………………13分
,
……………………………13分
与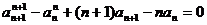 矛盾,
矛盾,
∴ 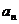 >
>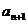 ……………………………………………14分
……………………………………………14分
22.(天津市武清区2009-2010学年高三下学期第一次模拟理)(本小题满分14分)
已知正项数列{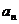 }满足
}满足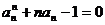 (
(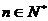 )
)
(1)求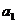 ,
,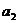 ;
;
(2)求证: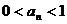
(3)求证: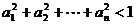 。
。
解: (1)∵ 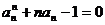 ,
,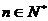
令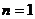 得
得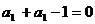 ∴
∴ 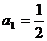 ………………1分
………………1分
令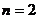 得
得
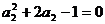 ∴
∴ 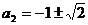
∵ 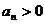 ∴
∴ 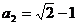 ……………………………3分
……………………………3分
(2)∵ 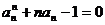 ∴
∴ 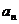 是方程
是方程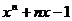 的一个根 ………4分
的一个根 ………4分
设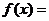
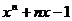 ,则
,则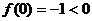 ,
,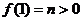 。
。
∴ 方程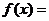 0在(0,1)内至少有一个根。
…………………6分
0在(0,1)内至少有一个根。
…………………6分
∵ 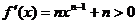 ∴
∴ 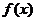 在(0,+∞)上是增函数,…………7分
在(0,+∞)上是增函数,…………7分
∴ 方程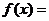 0在(0,+∞)上有唯一的根,且根在(0,1)内,
0在(0,+∞)上有唯一的根,且根在(0,1)内,
∴ 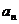 ∈(0,1) ∴
∈(0,1) ∴ 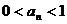 ………………………………9分
………………………………9分
(3)当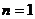 时,
时,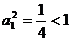 原式成立。………………………10分
原式成立。………………………10分
当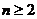 时,∵
时,∵
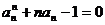 且
且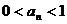
∴ 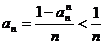 ……………………11分
……………………11分
∴ 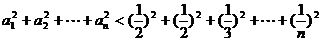
<
=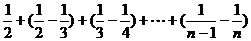
=1- ………………………………………13分
………………………………………13分
综上,∴ 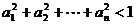 …………………………14分
…………………………14分
21. (天津市河西区2010届高三第一次模拟理科)(14分)
已知数列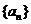 中,
中,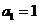 ,且点
,且点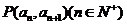 在直线
在直线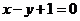 上。
上。
求数列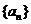 的通项公式;[来源:高&考%资(源#网
的通项公式;[来源:高&考%资(源#网
若函数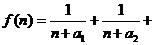 ……+
……+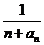
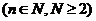 ,求函数
,求函数 的最小值;
的最小值;
设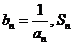 表示数列
表示数列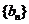 的前
的前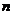 项和。试问:是否存在关于
项和。试问:是否存在关于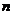 的模式
的模式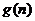 ,使得
,使得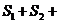 ……+
……+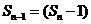 ·
·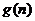 对于一切不小于2的自然数恒成立?若存在,写出
对于一切不小于2的自然数恒成立?若存在,写出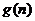 的解析式,并加以证明;若不存在,请说明理由。
的解析式,并加以证明;若不存在,请说明理由。

22.解:(Ⅰ)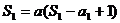 ∴
∴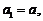 ………………1分
………………1分
当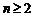 时,
时,
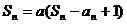
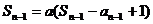
两式相减得: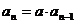 ,
,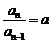
即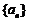 是等比数列.∴
是等比数列.∴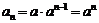 ;
……………………4分
;
……………………4分
(Ⅱ)由(Ⅰ)知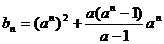 ,
,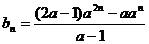 ,
,
若 为等比数列,则有
为等比数列,则有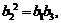 ……………………5分
……………………5分
而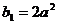 ,
,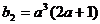 ,
,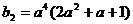 ……………………6分
……………………6分
故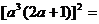
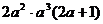 ,解得
,解得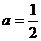 ,……………………………7分
,……………………………7分
再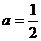 将代入得
将代入得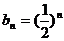 成立,
成立,
所以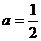 .
………………………………………………………………8分
.
………………………………………………………………8分
(III)证明:由(Ⅱ)知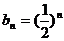 ,
,
所以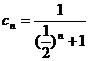
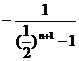 ,………………… 9分
,………………… 9分
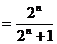
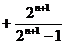
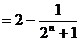
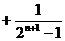 ……………… 11分
……………… 11分
所以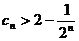
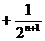 …………………… 12分
…………………… 12分
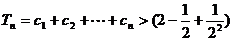
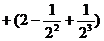
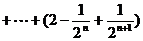

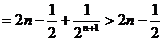 …………………………14分
…………………………14分
22.(天津十二区县重点中学2010年高三联考一理)(本小题满分14分)
已知数列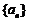 的前n项和
的前n项和 满足:
满足: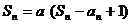 (
(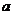 为常数,且
为常数,且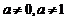 ).
).
(Ⅰ)求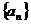 的通项公式;
的通项公式;
(Ⅱ)设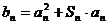 ,若数列
,若数列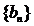 为等比数列,求
为等比数列,求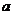 的值;
的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设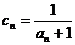
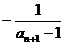 ,数列
,数列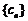 的前n项和为
的前n项和为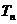 ,
,
求证: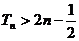 .
.
14.(天津市天津一中2010届高三第四次月考文科)五位同学围成一圈依次循环报数,规定:第一位同学首次报出的数为2,第二位同学首次报出的数为3,之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字,则第2010个被报出的数为 .4
16.(天津市武清区2009-2010学年高三下学期第一次模拟文)已知等差数列{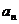 }的前
}的前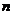 项和为
项和为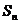 ,且满足
,且满足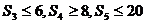 ,当
,当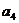 取得最大值时,数列{
取得最大值时,数列{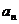 }的公差为
4
}的公差为
4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com