
18.(天津市武清区2009-2010学年高三下学期第一次模拟理)(本小题满分12分)
甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场。每场比赛胜者得3分,负者得0分,没有平局。在每一场比赛中,甲胜乙的概率为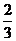 ,甲胜丙的概率为
,甲胜丙的概率为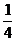 ,乙胜丙的概率为
,乙胜丙的概率为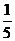 。
。
(1)求甲获第一名且丙获第二名的概率;
(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望。
解:(1)甲获第一,则甲胜乙且甲胜丙,
∴ 甲获第一的概率为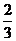 ×
×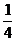 =
=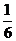 ………………2分
………………2分
丙获第二,则丙胜乙,其概率为1-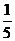 =
=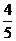 ………………4分
………………4分
∴ 甲获第一名且丙获第二名的概率为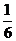 ×
×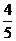 =
=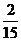 ……………6分
……………6分
(2)ξ可能取的值为0、3、6 …………………………7分
甲两场比赛皆输的概率为
P(ξ=0)=(1-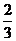 )(1-
)(1-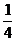 )=
)=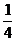 ………8分
………8分
甲两场只胜一场的概率为
P(ξ=3)=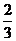 ×(1-
×(1-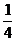 )+
)+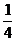 ×(1-
×(1-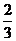 )=
)=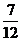 ………………9分
………………9分
甲两场皆胜的概率为P(ξ=6)=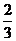 ×
×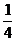 =
=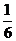 ……………10分
……………10分
∴ ξ的分布列为
|
ξ |
0 |
3 |
6 |
|
P |
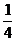 |
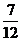 |
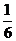 |
∴ Eξ=0×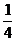 +3×
+3×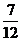 +6×
+6×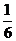 =
=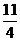 ……………………12分
……………………12分
18.(本题满分12分)
解:甲乙抽出卡片的所有可能情况:
|
甲 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
5 |
5 |
5 |
5 |
|
乙 |
2 |
3 |
4 |
5 |
1 |
3 |
4 |
5 |
1 |
2 |
4 |
5 |
1 |
2 |
3 |
5 |
1 |
2 |
3 |
4 |
共计20种结果。-------------------6分(可以不用表格)
(Ⅰ)甲抽到2的情况一共有4种情况,
所以甲抽到2的概率是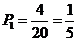 -----9分
-----9分
(Ⅱ)当甲比乙抽得的卡片上的数字大时甲获胜。由上表可知共有10种情况
所以甲获胜的概率为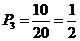 -----------12分
-----------12分
18.(天津十二区县重点中学2010年高三联考一文)(本小题满分12分)一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(Ⅰ)求第一次取到不合格品,且第二次取到的是合格品的概率;
(Ⅱ)求至少有一次取到不合格品的概率。
18.解:(Ⅰ)设选手甲第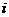 次击中目标的事件为
次击中目标的事件为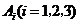 ,
,
则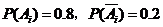
依题可知: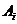 与
与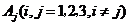 相互独立
相互独立
所求为: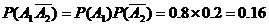 ………………5分
………………5分
(Ⅱ)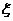 可能取的值为0,3,5,6.
………………6分
可能取的值为0,3,5,6.
………………6分
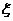 的分布列为:
的分布列为:
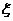 |
0 |
3 |
5 |
6 |
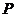 |
0.2 |
0.16 |
0.128 |
0.512 |
………………10分(表中的每一个概率值各占1分)
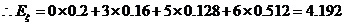 .………………12分
.………………12分
18. (天津十二区县重点中学2010年高三联考一理)(本小题满分12分)
某射击游戏规定:每位选手最多射击3次;射击过程中若击中目标,方可进行下一次射击,否则停止射击;同时规定第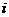
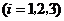 次射击时击中目标得
次射击时击中目标得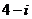 分,否则该次射击得
分,否则该次射击得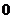 分。已知选手甲每次射击击中目标的概率为
分。已知选手甲每次射击击中目标的概率为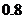 ,且其各次射击结果互不影响.
,且其各次射击结果互不影响.
(Ⅰ)求甲恰好射击两次的概率;
(Ⅱ)设该选手甲停止射击时的得分总和为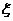 ,求随机变量
,求随机变量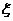 的分布列及数学期望.
的分布列及数学期望.
22. 解:(1)设数列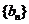 的公比为
的公比为 .由
.由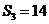 ,得
,得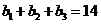 ;
;
由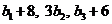 成等差数列,得
成等差数列,得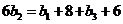 [来源:高&考%资(源#网]
[来源:高&考%资(源#网]
即 ,消去
,消去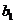 ,得
,得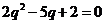 ,解得
,解得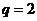 或
或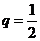 ,又因为
,又因为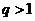 ,所以
,所以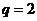 .将
.将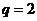 代入
代入 ,解得
,解得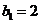 ,
,
所以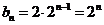
(1)由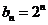 ,得
,得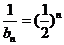 ,当
,当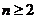 时,
时, ,当
,当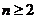 时,
时,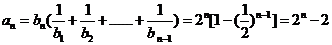 ,
,
所以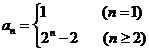 .
.
当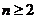 时,因为
时,因为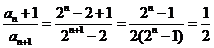 ;
;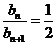
所以,当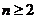 时,
时,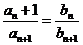 .
.
(3)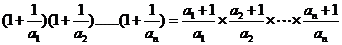
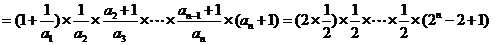
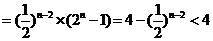 .
.
所以对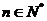 有
有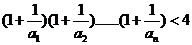 .
.
22.(天津市天津一中2010届高三第四次月考文科)已知数列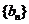 是公比大于1的等比数列,
是公比大于1的等比数列,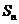 数列
数列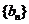 的前
的前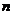 项和,满足
项和,满足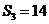 ,且
,且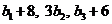 构成等差数列,数列
构成等差数列,数列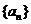 满足:
满足: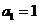 ,
,
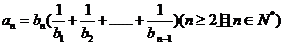 .
.
(1)求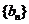 的通项公式
的通项公式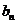 ;
;
(2)证明: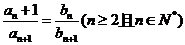 ;
;
(3)求证: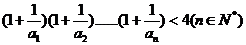 .
.
22、解:(1)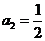 ,
, 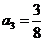 ,
,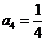 ……………………(2分)
……………………(2分)
由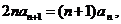 得
得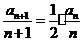 ……………………(3分)
……………………(3分)
即数列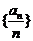 是以
是以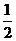 为首项,以
为首项,以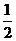 为公比的等比数列
为公比的等比数列
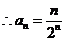 ……………………(4分)
……………………(4分)
注:用数学归纳法也可以。
(2)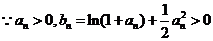
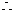 要证明
要证明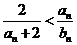 只需证明
只需证明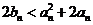
即证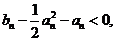 即证明
即证明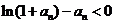 成立……………………(6分)
成立……………………(6分)
构造函数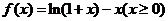 ……………………(7分)
……………………(7分)
则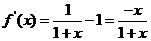 ,……………………(8分)
,……………………(8分)
当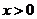 时,
时,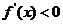 ,即
,即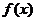 在
在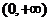 上单调递减,所以
上单调递减,所以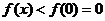
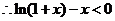 ,即
,即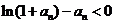 对一切
对一切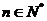 都成立,
都成立,
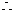
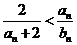 ……………………(10分)
……………………(10分)
(3)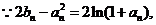
由(2)可知
 ……………………(12分)
……………………(12分)
利用错位相减法求得
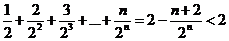
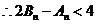 ……………………(14分)
……………………(14分)
22.(天津市天津一中2010届高三第四次月考理科)设数列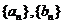 满足
满足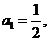
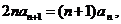 且
且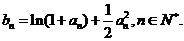
(1)求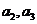 ,
,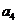 并求数列
并求数列
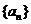 的通项公式;
的通项公式;
(2)对一切 ,证明
,证明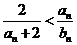 成立;
成立;
(3)记数列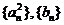 的前
的前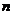 项和分别是
项和分别是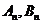 ,证明
,证明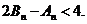
20.解:(1)因为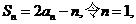
解得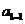 …………1分
…………1分
再分别令n=2,n=3,解得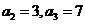 …………3分
…………3分
(2)因为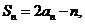
所以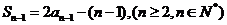
两式相减得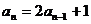
所以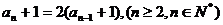
又因为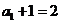 ,所以
,所以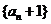 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
所以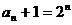 ,所以
,所以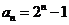 …………7分
…………7分
(3)因为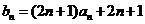 ,
,
所以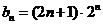
所以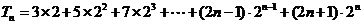 ①
①
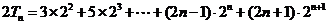 ②
②
①-②得:
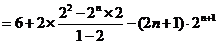
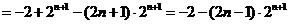
所以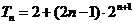 …………10分
…………10分
若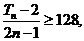
则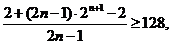
即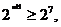 所以
所以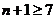 ,解得
,解得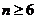 ,
,
所以满足不等式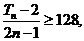 的最小n值6, …………12分
的最小n值6, …………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com