
19.(本小题满分12分)解法一 向量法
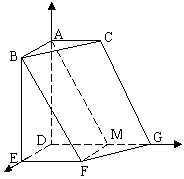 由已知,AD、DE、DG两两垂直,建立如图的坐标系,
由已知,AD、DE、DG两两垂直,建立如图的坐标系,
则A(0,0,2),B(2,0,2),C(0,1,2),
E(2,0,0),G(0,2,0),F(2,1,0)
(Ⅰ)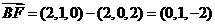
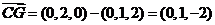
∴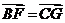 ,所以BF∥CG.
,所以BF∥CG.
又BF 平面ACGD
平面ACGD
故 BF//平面ACGD……………………4分
(Ⅱ)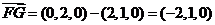 ,
,
设平面BCGF的法向量为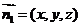 ,
,
则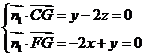 ,
,
令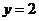 ,则
,则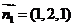 ,
,
而平面ADGC的法向量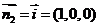
∴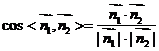 =
=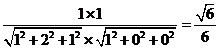
 故二面角D-CG-F的余弦值为
故二面角D-CG-F的余弦值为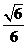 .……………………8分
.……………………8分
(Ⅲ)设DG的中点为M,连接AM、FM,
则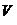 =
=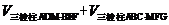
=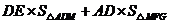 =
=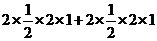 =
=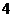 .……………12分
.……………12分
解法二设DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,
所以MF//DE,且MF=DE
又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF 平面ACGD
平面ACGD
故 BF//平面ACGD……………4分
(利用面面平行的性质定理证明,可参照给分)
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG
即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
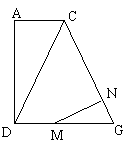 ∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴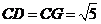 ,
∴MN=
,
∴MN=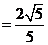
在直角三角形MNF中,MF=2,MN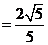
∴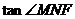 =
=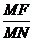 =
=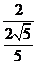 =
=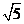 ,
, =
=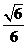
故二面角D-CG-F的余弦值为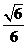 ……………………8分
……………………8分
(Ⅲ) =
=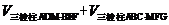 =
=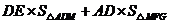
=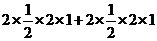 =
=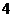 .……………12分
.……………12分
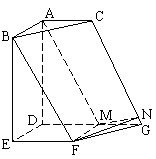
19.(天津十二区县重点中学2010年高三联考一理)(本小题满分12分)
如图,在六面体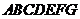 中,平面
中,平面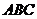 ∥平面
∥平面 ,
,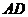 ⊥平面
⊥平面 ,
,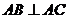 ,
,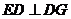 ,
,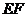 ∥
∥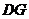 .且
.且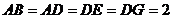 ,
,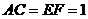 .
.
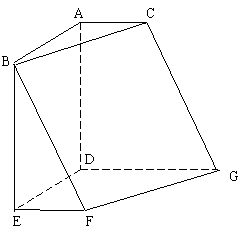 (Ⅰ)求证:
(Ⅰ)求证: 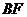 ∥平面
∥平面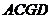 ;
;
(Ⅱ)求二面角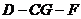 的余弦值;
的余弦值;
(Ⅲ) 求五面体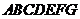 的体积.
的体积.
16.(天津市天津一中2010届高三第四次月考理科)在棱长为2的正方体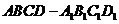 中,正方形
中,正方形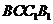 所在平面内的动点
所在平面内的动点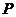 到直线
到直线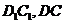 的距离之和为
的距离之和为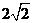 ,则
,则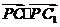 有最大值
.
有最大值
.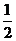
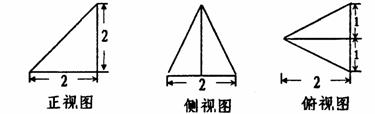
14. (天津市天津一中2010届高三第四次月考理科)已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
. 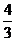
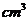
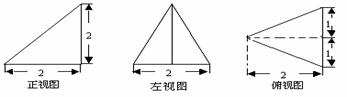
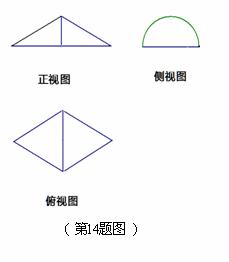
12.(天津市六校2010届高三第三次联考文科)已知某几何体的三视图如图所示,则该几何体的表面积为
. 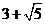
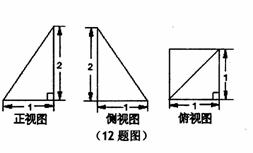
14.(天津市六校2010届高三第三次联考理科)已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),则这个几何体的体积是
cm3. 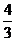
14.(天津十二区县重点中学2010年高三联考一理)某几何体的三视图,其中正视图是腰长为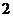 的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
.
的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
.
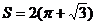
10.(天津市天津一中2010届高三第四次月考文科) 在正四棱柱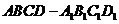 中,顶点
中,顶点 到对角线
到对角线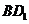 和到平面
和到平面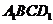 的距离分别为
的距离分别为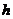 和
和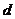 ,则下列命题中正确的是( C )
,则下列命题中正确的是( C )
A.若侧棱的长小于底面的边长,则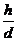 的取值范围为
的取值范围为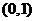
B.若侧棱的长小于底面的边长,则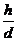 的取值范围为
的取值范围为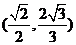 [来源:高&考%资(源#网]
[来源:高&考%资(源#网]
C.若侧棱的长大于底面的边长,则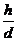 的取值范围为
的取值范围为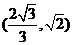
D.若侧棱的长大于底面的边长,则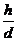 的取值范围为
的取值范围为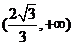
5.(天津市天津一中2010届高三第四次月考理科)设三条不同的直线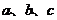 ,两个不同的平面
,两个不同的平面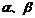 ,
,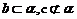 。则下列命题不成立的是( B )
。则下列命题不成立的是( B )
A.若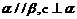 ,则
,则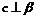 B.“若
B.“若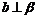 ,则
,则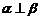 ”的逆命题
”的逆命题
C.若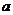 是
是 在
在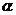 的射影,
的射影,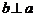 则
则 D.“若
D.“若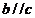 ,则
,则 ”的逆否命题
”的逆否命题
8.(天津市武清区2009-2010学年高三下学期第一次模拟文)在空间四边形ABCD中,E、F分别为AC、BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为( D )
A.900 B.600
C.450 D.300
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com