
3.设m,n是两条不同的直线,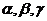 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题:
①若m⊥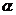 ,n∥
,n∥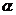 ,则m⊥n;②若
,则m⊥n;②若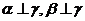 则
则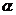 ∥
∥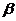 ;
;
③若m∥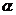 ,n∥
,n∥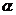 ,则m∥n;④若
,则m∥n;④若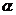 ∥
∥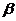 ,
,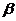 ∥
∥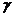 , m⊥
, m⊥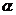 则m⊥
则m⊥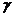 .
.
其中正确命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
2.用小立方体搭一个几何体,使得它的主视图和俯视图如图所示。这样的几何体需要的小立方块最少与最多分别是 ( )

A. 10与15 B.9与17
C.10与16 D.9与16
1.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、
右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方
体的上面,则这个正方体的下面是 ( )
A. 0 B. 7 C.快 D.乐
22.(本小题满分14分)
已知函数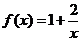 ,数列
,数列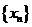 满足
满足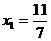 ,
,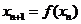 ;若
;若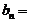
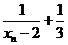 .
.
(1)求证数列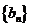 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)若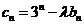 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有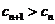 成立.
成立.
21.(本小题满分12分)
已知数列{a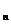 }中,
}中,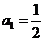 ,且
,且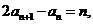 其中n=1,2,3…;若
其中n=1,2,3…;若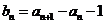 ,
,
(1)求证:数列{b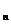 }是等比数列;
}是等比数列;
(2)求数列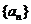 的通项
的通项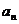 .
.
20.(本小题满分12分)
已知单调递增的等比数列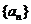 满足:
满足: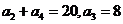 ;
;
(1)求数列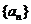 的通项公式;
的通项公式;
(2)若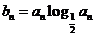 ,数列
,数列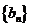 的前n项和为
的前n项和为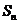 ,求
,求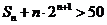 成立的正整数 n的最小值.
成立的正整数 n的最小值.
19.(本小题满分12分)
已知数列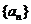 的各项均为正数,
的各项均为正数,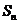 为其前
为其前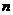 项和,且对任意的
项和,且对任意的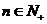 ,有
,有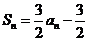 .
.
(1)求数列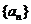 的通项公式;
的通项公式;
(2)设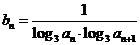 ,求数列
,求数列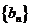 的前
的前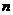 项和
项和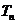 .
.
18.(本小题满分12分)
已知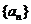 是首项为1,公差为1的等差数列;若数列
是首项为1,公差为1的等差数列;若数列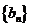 满足
满足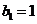 ,
,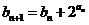 .
.
(1)求数列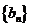 的通项公式;
的通项公式;
(2)求证: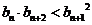 .
.
17.(本小题满分12分)
已知数列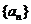 是一个等差数列,且
是一个等差数列,且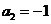 ,
,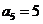 .
.
(1)求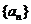 的通项
的通项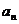 ;
;
(2)求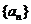 前n项和
前n项和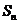 的最小值.
的最小值.
16.甲型h1n1流感病毒是寄生在宿主的细胞内的,若该细胞开始时2个,记为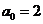 ,它们按以下规律进行分裂,1 小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1 个,……,记n小时后细胞的个数为
,它们按以下规律进行分裂,1 小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1 个,……,记n小时后细胞的个数为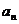 ,则
,则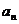 =________(用n表示) .
=________(用n表示) .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com