
1.学已知复数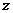 满足
满足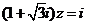 ,则
,则 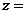 ( )
( )
A.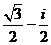 B.
B.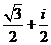 C.
C.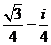 D.
D.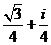
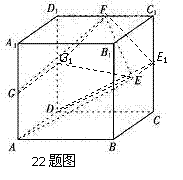
22.(14分) 如图,已知正方体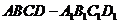 的棱长为2,点
的棱长为2,点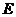 是正方形
是正方形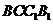 的中心,点
的中心,点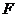 、
、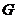 分别是棱
分别是棱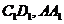 的中点.设点
的中点.设点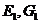 分别是点
分别是点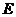 ,
,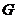 在平面
在平面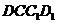 内的正投影.
内的正投影.
(1)求以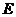 为顶点,以四边形
为顶点,以四边形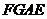 在平面
在平面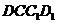 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线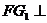 平面
平面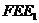 ;
;
 (3)求异面直线
(3)求异面直线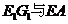 所成角的正弦值.
所成角的正弦值.
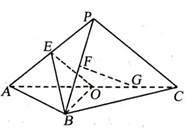
21.(本小题满分12分) 数学课上,张老师用六根长度均为a的塑料棒搭成了一个正三棱锥(如图所示),然后他将其中的两根换成长度分别为在 和
和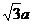 的塑料棒、又搭成了一个三棱锥,陈成同学边听课边动手操作,也将其中的两根换掉,但没有成功,不能搭成三棱锥,如果两人都将BD换成了长为
的塑料棒、又搭成了一个三棱锥,陈成同学边听课边动手操作,也将其中的两根换掉,但没有成功,不能搭成三棱锥,如果两人都将BD换成了长为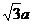 的塑料棒.
的塑料棒.
(1)试问张老师换掉的另一根塑料棒是什么,而陈成同学换掉的另一根塑料棒又是什么?请你用学到的数学知识解释陈成同学失败的原因;
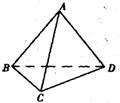 (2)试证:平面ABD⊥平面CBD;
(2)试证:平面ABD⊥平面CBD;
(3)求新三棱锥的外接球的表面积.
20.已知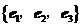 为空间的一个基底,且
为空间的一个基底,且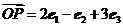 ,
,
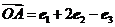 ,
,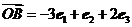 ,
,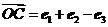 .
.
(1)判断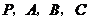 四点是否共面;
四点是否共面;
(2)能否以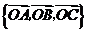 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量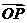 .
.
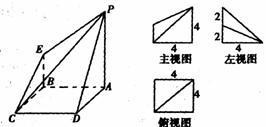
19. (12分)下图是一几何体的直观图、主视图、俯视图、左视图.
(1)若F为PD的中点,求证:AF⊥面PCD;
(2)证明BD∥面PEC;
(3)求面PEC与面PDC所成的二面角(锐角)的余弦值.
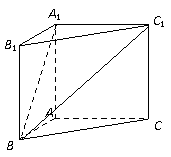
18.在直三棱柱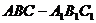 中,
中,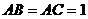 ,
,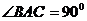 ,且异面直线
,且异面直线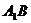 与
与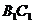 所成的角等于
所成的角等于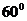 ,设
,设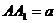 .
.
(1)求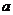 的值;
的值;
 (2)求平面
(2)求平面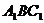 与平面
与平面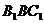 所成的锐二面角的大小.
所成的锐二面角的大小.
17.(12分)(09浙江理20)如图,平面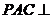 平面
平面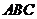 ,
,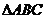 是以
是以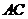 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,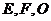 分别为
分别为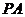 ,
,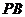 ,
,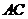 的中点,
的中点,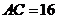 ,
,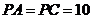 .
.
(I)设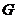 是
是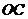 的中点,证明:
的中点,证明: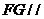 平面
平面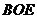 ;
;
(II)证明:在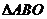 内存在一点
内存在一点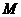 ,使
,使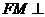 平面
平面 ,并求点
,并求点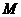 到
到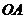 ,
,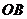 的距离.
的距离.
16.下列命题:
①若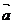 与
与 共线,
共线,  与
与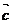 共线,则
共线,则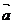 与
与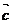 共线;
共线;
②向量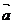 、
、 、
、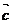 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③若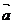 与
与 共线,则存在唯一的实数
共线,则存在唯一的实数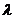 ,使
,使 =
=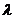
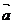 ;
;
④若A、B、C三点不共线,0是平面ABC外一点.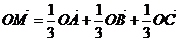 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,
上述命题中的真命题是 .
15. 已知球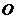 的半径为1,
的半径为1,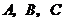 三点都在球面上,且每两点间的球面距离为
三点都在球面上,且每两点间的球面距离为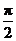 ,则球心
,则球心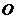 到平面
到平面 的距离为
,
的距离为
,
14. 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
1的正方体内,使正四棱锥的底面ABCD与正方体的某一个
平面平行,且各顶点均在正方体的面上,则这样的
几何体体积的可能值有 个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com