
5.同时抛掷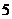 枚均匀的硬币
枚均匀的硬币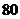 次,设
次,设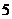 枚硬币正好出现
枚硬币正好出现 枚正面向上,
枚正面向上,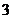 枚反面向上的次数为
枚反面向上的次数为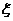 ,则
,则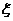 的数学期望是 ( )
的数学期望是 ( )
A.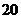 B.
B. C.
C.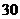 D.
D.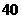
4.在二项式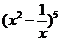 的展开式中,含
的展开式中,含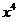 的项的系数是 ( )
的项的系数是 ( )
A.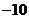 B.
B.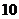 C.
C.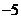 D.
D.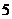
3.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了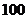 位居民进行调查,经过计算
位居民进行调查,经过计算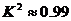 ,根据这一数据分析,下列说法正确的是 ( )
,根据这一数据分析,下列说法正确的是 ( )
A.有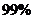 的人认为该栏目优秀
的人认为该栏目优秀
B.有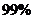 的人认为该栏目是否优秀与改革有关系
的人认为该栏目是否优秀与改革有关系
C.有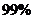 的把握认为电视栏目是否优秀与改革有关系
的把握认为电视栏目是否优秀与改革有关系
D.没有理由认为电视栏目是否优秀与改革有关系
2.某单位有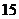 名成员,其中男性
名成员,其中男性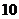 人,女性
人,女性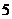 人,现需要从中选出
人,现需要从中选出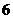 名成员组成考察团外出参观学习,如果按性别分层,并在各层按比例随机抽样,则此考察团的组成方法种数是 (
)
名成员组成考察团外出参观学习,如果按性别分层,并在各层按比例随机抽样,则此考察团的组成方法种数是 (
)
A.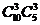 B.
B.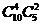 C.
C.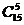 D.
D.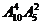
1.正态总体的概率密度函数为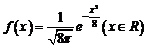 ,则总体的平均数和标准差分别是
,则总体的平均数和标准差分别是
( )
A.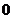 和
和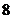 B.
B.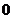 和
和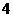 C.
C.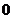 和
和 D.
D.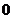 和
和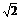
22.(14分)
设椭圆E: 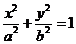 (a,b>0)过M(2,
(a,b>0)过M(2,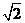 )
,N(
)
,N(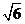 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,
且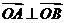 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理
21.(12分)如图,已知椭圆的中心在原点,焦点在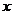 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在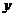 轴上的截距为
轴上的截距为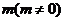 ,l交椭圆于A、B两个不同点.
,l交椭圆于A、B两个不同点.
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与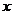 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
20.(12分)
已知椭圆G的中心在坐标原点,长轴在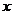 轴上,离心率为
轴上,离心率为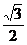 ,两个焦点分别为
,两个焦点分别为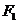 和
和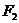 ,椭
,椭
圆G上一点到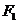 和
和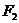 的距离之和为12.圆
的距离之和为12.圆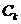 :
: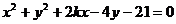
 的圆心为点
的圆心为点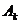 .
.
(1)求椭圆G的方程
(2)求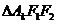 的面积
的面积
(3)问是否存在圆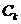 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
19.(12分)双曲线的中心为原点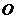 ,焦点在
,焦点在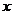 轴上,两条渐近线分别为
轴上,两条渐近线分别为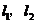 ,经过右焦点
,经过右焦点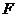 垂直于
垂直于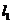 的直线分别交
的直线分别交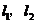 于
于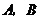 两点.已知
两点.已知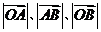 成等差数列,且
成等差数列,且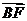 与
与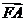 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设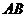 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
18.(12分)已知一动圆M,恒过点F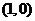 ,且总与直线
,且总与直线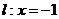 相切.
相切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)探究在曲线C上,是否存在异于原点的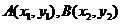 两点,当
两点,当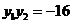 时,
时,
直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com