
3. 质量为2千克的物体,受到一个平行于斜面向上,大小为7N的拉力F而静止在倾角为370的斜面上,若斜面与物体间的摩擦因数为0.4,则物体受到的摩擦力是
A.6.4N B.8N C.5N D.12N
2. 几个共点力作用在一个质点上,使质点处于平衡状态,当其中的F1逐渐
减小而其他力不变时,物体所受的合力
A. 逐渐增大,与F1同向 B. 逐渐增大,与F1反向
C. 逐渐减少,与F1同向 D. 逐渐减少,与F1反向
个选项是正确的)
1.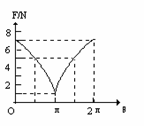 有两个互成角度的共点力,夹角为θ,它们的合力的大小随θ的变化关系如图所示。那么,这两个力的大小分别是
有两个互成角度的共点力,夹角为θ,它们的合力的大小随θ的变化关系如图所示。那么,这两个力的大小分别是
A. 3N、4N B.2N、5N C. 1N、6N D.3.5N、3.5N
尝试指导与合作交流相结合,通过提出问题,观察实例,引导学生理解掌握两条直线平行与垂直的判定方法.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
复习引入 |
上一节课,我们已经学习了直线的倾斜角和斜率的概念,而且知道,可以用倾斜角和斜率来表示直线相对于x轴的倾斜程度,并推导出了斜率的坐标计算公式.现在,我们来研究能否通过两条直线的斜率来判断两条直线的平行或垂直. |
由学生回忆上节课内容,再由老师引入新课. |
设置情境引入新课 |
|
概念形成 |
1.特殊情况下,两条直线平行与垂直. 两条直线中有一条直线没有斜率,(1)当另一条直线的斜率也不存在时,两直线的倾斜角都为90°,它们互相平行;(2)当另一条直线的斜率为0时,一条直线的倾斜角为90°,另一条直线的倾斜角为0° ,两直线互相垂直. |
由学生讨论得出答案 |
|
|
概念深化 |
2.两条直线的斜率都存在时,两直线的平行与垂直. 设直线l1和l2的斜率分别为k1和k2.我们知道,两条直线的平行或垂直是由两条直线的方向决定的,而两条直线的方向又是由直线的倾斜角或斜率决定的,所以我们下面要研究的问题是:两条互相平行或垂直的直线,它们的斜率有什么关系?  首先研究两条直线互相平行(不重合)的情形.如果l1∥l2(图),那么它们的倾斜角相等;a1 = a2.(借助计算机,让学生通过度量,感知a1,a2的关系)  ∴tga1 = tga2.  即k1 = k2.  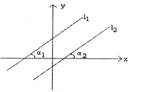  反过来,如果两条直线的斜率相等:即k1 = k2,那么tga1 = tga2.  由于0°≤a1<180°,0°≤a<180°,  ∴a1 = a2  又∵两条直线不重合,  ∴l1∥l2.  结论:两条直线都有斜率而且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,那么它们平行,即l1∥l2  k1 = k2. k1 = k2. 注意:上面的等价是在两条直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不成立.即如果k1 = k2那么一定有l1∥l2;反之则不一定. |
借助计算机,让学生通过度量,感知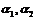 的关系. 的关系. |
通过斜率相等判定两直线平行,是通过代数方法得到几何结论,体现了用代数方法研究几何问题的思想. |
下面我们研究两条直线垂直的情形. 如果l1⊥l2,这时 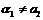 ,否则两直线平行. ,否则两直线平行. 设 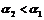 (图)甲图的特征是l1与l2的交点在x轴上方;乙图的特征是l1与l2的交点在x轴下方;丙图的特征是l1与l2的交点在x轴上,无论哪种情况下都有 (图)甲图的特征是l1与l2的交点在x轴上方;乙图的特征是l1与l2的交点在x轴下方;丙图的特征是l1与l2的交点在x轴上,无论哪种情况下都有 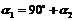 . . 因为l1、l2的斜率分别是k1、k2,即 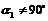 ,所以 ,所以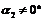 . . ∴ 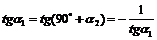 . . 即 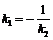 或k1k2
= –1, 或k1k2
= –1, 反过来,如果 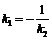 即k1·k2 = –1不失一般性,设k1<0. 即k1·k2 = –1不失一般性,设k1<0. k2>0,  那么 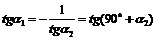 . . 可以推出a1 = 90°+ 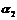 . . l1⊥l2. 结论:两条直线都有斜率,如果它们互相垂直,那么它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,那么它们互相垂直,即 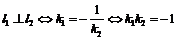 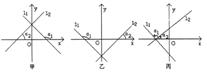 注意:结论成立的条件,即如果k1·k2 = –1,那么一定有l1⊥l2;反之则不一定. |
借助计算机,让学生通过度量,感知k1,k2的关系,并使l1(或l2)转动起来,但仍保持l1⊥l2,观察k1,k2的关系,得到猜想,再加以验证,可使为锐角,钝角等. |
通过计算机的演示,培养学生的观察、猜想,归纳的数学思想方法. |
|
|
应用举例 |
例1 已知A (2,3),B (–4,0),P(– 3,1),Q(–1,2),试判断直线BA与PQ的位置关系,并证明你的结论. |
借助计算机作图,使学生通过观察猜想:BA∥PQ,再通过计算机加以验证.(图略) 例1 解:直线BA的斜率k1 = (3 – 0)/(2 – (–4)) = 0.5, 直线PQ的斜率k2 = (2 – 1)/( –1 – (–3)) = 0.5, 因为k1 = k2 = 0.5,所以直线BA∥PQ. |
通过例题的讲解,使学生进一步理解掌握直线平行与垂直的条件. |
|
例2 已知四边形ABCD的四个顶点分别为A(0,0),B (2, –1),C (4,2),D (2,3),试判断四边形ABCD的形状,并给出证明. 例3 已知A(–6,0),B (3,6),P (0,3),Q (–2,6),试判断直线AB与PQ的位置关系. 例4 已知A(5, –1),B (1,1),C (2,3),试判断三角形ABC的形状. 分析:借助计算机作图,通过观察猜想:三角形ABC是直角三角形,其中AB⊥BC,再通过计算加以验证.(图略) 课堂练习 P94 练习1、2. |
借助计算机作图,使学生通过观察猜想:四边形ABCD是平行四边形,再通过计算加以验证. 例2 解:直线BA的斜率k1 = (3 – 0)/(2 – (–4)) = 0.5, 直线PQ的斜率k2 = (2 – 1)/( –1 – (–3)) = 0.5, 因为k1 = k2 = 0.5,所以直线BA∥PQ. 例3 解:直线AB的斜率k1 = (6 – 0)/ (3 – (–6)) = 2/3, 直线PQ的斜率k2 = (6 – 3) (–2 – 0) = 3/2, 因为k1·k2 = –1,所以AB⊥PQ. |
||
|
归纳总结 |
(1)两条直线平行或垂直的真实等价条件; (2)应用条件,判定两条直线平行或垂直. (3)应用直线平行的条件,判定三点共线. |
由学生归纳,教师再补充完善. |
培养学生的概括能力 |
|
课后作业 |
见习案3.1的第二课时 |
由学生独立完成 |
巩固深化新学知识 |
备选例题
例1 试确定M的值,使过点A(m + 1,0),B(–5,m)的直线与过点C(–4,3),D(0,5)的直线平行.
[解析]由题意得:
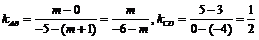
由于AB∥CD,即kAB = kCD,
所以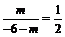 ,所以m = –2.
,所以m = –2.
例2 已知长方形ABCD的三个顶点的坐标分别为A (0,1),B (1,0),C (3,2),求第四个顶点D的坐标.
[解析]设第四个顶点D的坐标为(x,y)
因为AD⊥CD,AD∥BC 所以kAD·kCD = –1,且kAD = kBC
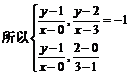 ,
,
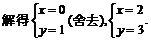
所以第四个顶点D的坐标为(2,3).
例3 已知定点A(–1,3),B(4,2),以A、B为直径的端点,作圆与x轴有交点C,求交点C的坐标.
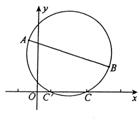 [解析]以线段AB为直径的圆与x轴交点为C.
[解析]以线段AB为直径的圆与x轴交点为C.
则AC⊥BC,设C (x,0)
则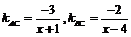
所以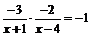
所以x = 1或2,所以C (1,0)或(2,0)
重点:两条直线平行和垂直的条件.
难点:启发学生,把研究两条直线的平行或垂直问题,转化为研究两条直线的斜率的关系问题.
3.情感、态度与价值观
通过对两直线平行与垂直的位置关系的研究,培养学生的成功意识,合作交流的学习方式,激发学生的学习兴趣.
2.过程与方法
通过探究两直线平行或垂直的条件,培养学生运用正确知识解决新问题的能力,以及数形结合能力.
1.知识与技能
理解并掌握两条直线平行与垂直的条件,会运用条件判定两直线是否平行或垂直.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
提出问题引入 |
我们知道,经过两点有且只有(确定)一条直线,那么,经过一点P的直线l的位置能确定吗?如图,过一点P可作无数多条直线a,b,c,…易见,答案是否定的,这些直线有什么联系呢? 直线的倾斜角的概念. |
学生回答(不能确定) (1)它们都经过点P.  (2)它们的倾斜程度不同.  接着教师提出:怎样描述这种倾斜程度的不同?由此引入课题. |
设疑激趣导入课题 |
|
概念形成 |
1.直线倾斜角的概念 当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角 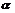 叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时,规定 叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时,规定 . . |
教师提问: 倾斜角 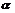 的取值范围是什么? 的取值范围是什么?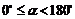  当直线l与x轴重合时 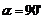  (由学生结合图形回答) |
|
|
概念深化 |
因为平面直角坐标系内的每一条直线都有确定的倾斜程度,引入直线的倾斜角之后,我们就可以用倾斜角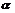 来表示平面直角坐标系内的每一条直线的倾斜程度. 来表示平面直角坐标系内的每一条直线的倾斜程度. 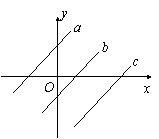  确定平面直角坐标系内的一条直线位置的几何要素:一个点P和一个倾斜角 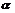 . . |
教师提问: 如左图,直线a∥b∥c,那么它们的倾斜角 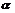 相等吗? 相等吗? 学生回答后作出结论.  一个倾斜角 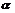 不能确定一条直线,进而得出. 确定一条直线位置的几何要素. 不能确定一条直线,进而得出. 确定一条直线位置的几何要素. |
通过这种师生互动引导学生明确确定一条直线位置的两个几何要素 |
|
概念形成 |
2.直线的斜率 一条直线的倾斜角 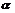 ( (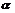 ≠90°)的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即 ≠90°)的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即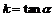 . . 由此可知,一条直线l的倾斜角 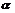 一定存在,但是斜率k不一定存在. 例如 一定存在,但是斜率k不一定存在. 例如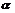 = 45°时 = 45°时 k = tan45°= 1  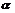 = 135°时 k = tan135°= –1 = 135°时 k = tan135°= –1 |
教师提问:(由学生讨论后回答) (1)当直线l与x轴平行或重合时,k为多少? k = tan0°= 0 (2)当直线l与x轴垂直时,k还存在吗? 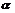 = 90°,k不存在 = 90°,k不存在 |
设疑激发学生思考得出结论 |
|
概念形成 |
3.直线的斜率公式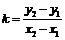 对于上面的斜率公式要注意下面四点: (1)当x1 = x2时,公式右边无意义,直线的斜率不存在,倾斜角 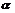 = 90°,直线与x轴垂直; = 90°,直线与x轴垂直;(2)k与P1、P2的顺序无关,即y1、y2和x1、x2在公式中的前后次序可以同时交换,但分子与分母不能交换; (3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得; (4)当y1 = y2时,斜率k = 0,直线的倾斜角 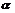 = 0°,直线与x轴平行或重合. = 0°,直线与x轴平行或重合.(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到. |
教师提出问题: 给定两点P1 (x1,y1),P2 (x2,y2),x1≠x2,如何用两点的坐标来表示直线P1、P2的斜率? 可用计算机作动画演示:直线P1P2的四种情况,并引导学生如何作辅助线,共同完成斜率公式的推导. |
借助多媒体演示让学生亲自体会斜率公式的推导过程. |
|
应用举例 |
例1 已知A (3,2),B (–4,1),C (0,–1),求直线AB,BC,CA的斜率,并判断它们的倾斜角是钝角还是锐角.(用计算机作直线,图略) 分析:已知两点坐标,而且x1 ≠ x2,由斜率公式代入即可求得k的值; 而当  时,倾斜角 时,倾斜角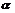 是钝角; 是钝角;而当  时,倾斜角 时,倾斜角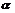 是锐角; 是锐角;而当  时,倾斜角 时,倾斜角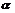 是0°. 是0°.例2 在平面直角坐标系中,画出经过原点且斜率分别为1,–1,2及–3的直线a,b,c,1. 分析:要画出经过原点的直线a,只要再找出a上的另个一点M.而M的坐标可以根据直线a的斜率确定;或者k = tan 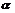 =1是特殊值,所以也可以以原点为角的顶点,x轴的正半轴为角的一边,在x轴的上方作45°的角,再把所作的这一边反向延长成直线即可. =1是特殊值,所以也可以以原点为角的顶点,x轴的正半轴为角的一边,在x轴的上方作45°的角,再把所作的这一边反向延长成直线即可. |
学生分析求解 ,教师板书 例1 略解:直线AB的斜率k1 = 1/7>0,所以它的倾斜角是锐角. 直线BC的斜率k2 = –0.5<0,所以它的倾斜角是锐角. 例2 略解:设直线a上的另个一点M的坐标为(x,y),根据斜率公式有1 = (y – 0)/(x – 0) 所以 x = y 可令x = 1,则y = 1,于是点M的坐标为(1,1).此时过原点和点M(1,1),可作直线a. 同理,可作直线b,c,1.(用计算机作动画演示画直线过程) 课堂练习:P91 1题、2题、3题、4题. |
通过应用进一步理解倾斜角,斜率的有关定义 |
|
归纳总结 |
(1)直线的倾斜角和斜率的概念. (2)直线的斜率公式. |
师生共同总结--交流--完善 |
引导学生学会自己总结 |
|
课后作业 |
布置作业 见习案3.1第一课时 |
由学生独立完成 |
巩固深化 |
备选例题
例1 求下列两点直线的斜率,并判断其倾斜角是锐角还是钝角.
(1)(1,1),(2,4); (2)(–3,5),(0,2);
(3)(2,3),(2,5); (4)(3,–2),(6,–2)
[解析](1)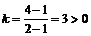 ,所以倾斜角是锐角;
,所以倾斜角是锐角;
(2) ,所以倾斜角是钝角;
,所以倾斜角是钝角;
(3)由x1 = x2 = 2得:k不存在,倾斜角是90°
(4)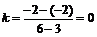 ,所以倾斜角为0°
,所以倾斜角为0°
例2 已知点P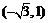 点Q在y轴上,直线PQ的倾斜角为120°,则Q点的坐标为 .
点Q在y轴上,直线PQ的倾斜角为120°,则Q点的坐标为 .
[解析]因为点Q在y轴上,则可设其坐标为(0,6)
直线PQ的斜率k = tan120°= 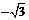
∴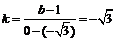 ∴b = –2,即Q点坐标为
∴b = –2,即Q点坐标为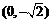
直线的倾斜角、斜率的概念和公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com