
10.设a=log0.70.8,b=log1.10.9,c=1.10.9,那么( )
A.a<b<c B.a<c<b
C.b<a<c D.c<a<b
[解析] a=log0.70.8>0,且a=log0.70.8<log0.70.7=1.
b=log1.10.9<log1.11=0.
c=1.10.9>1.
∴c>1>a>0>b.即b<a<c.故选C.
[答案] C
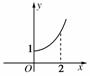
9.定义在R上的偶函数f(x)的部分图象如右图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是( )
A.y=x2+1 B.y=|x|+1
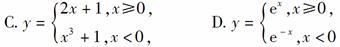
[解析] 利用偶函数的对称性知f(x)在(-2,0)上为减函数.又y=x2+1在(-2,0)上为减函数;y=|x|+1在(-2,0)上为减函数;y=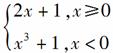 在(-2,0)上为增函数.
在(-2,0)上为增函数.
y=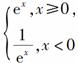 在(-2,0)上为减函数.故选C.
在(-2,0)上为减函数.故选C.
[答案] C
8.设f(x)=3x-x2,则在下列区间中,使函数f(x)有零点的区间是( )
A.[0,1] B.[1,2]
C.[-2,-1] D.[-1,0]
[解析] ∵f(-1)=3-1-(-1)2=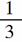 -1=
-1=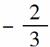 <0,f(0)=30-02=1>0,
<0,f(0)=30-02=1>0,
∴f(-1)·f(0)<0,∴有零点的区间是[-1,0].
[答案] D
7.若函数f(x)=x2+2x+3a没有零点,则实数a的取值范围是( )

[解析] 由题意,函数f(x)=x2+2x+3a没有零点,即方程x2+2x+3a=0无解,即方程的判别式小于零,解不等式Δ=b2-4ac=22-4×3a<0,解得a>\f(1,3).
[答案] B
6.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x).则f(6)的值为( )
A.-1 B.0
C.1 D.2
[解析] ∵f(x)为奇函数,∴f(0)=0.
又∵f(x+2)=-f(x),
∴f(2)=-f(0)=0.
∴f(4)=-f(2)=0,
∴f(6)=-f(4)=0.故应选B.
[答案] B
5.幂函数的图象经过点(2,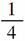 ),则它的单调递增区间是( )
),则它的单调递增区间是( )
A.(0,+∞) B.[0,+∞)
C.(-∞,0) D.(-∞,+∞)
[解析] 设y=xn,则2n=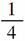 ,∴n=-2.∴幂函数是y=x-2,故应选C.
,∴n=-2.∴幂函数是y=x-2,故应选C.
[答案] C
4.已知函数f(x)=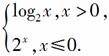 若f(a)=\f(1,2),则a=( )
若f(a)=\f(1,2),则a=( )

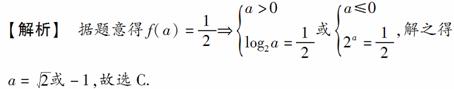
[答案] C
3.若不等式x2-x≤0的解集为M,函数f(x)=ln(1-|x|)的定义域为N,则M∩N为( )
A.[0,1) B.(0,1)
C.[0,1] D.(-1,0]
[解析] 不等式x2-x≤0的解集M={x|0≤x≤1},f(x)=ln(1-|x|)的定义域N={x|-1<x<1},
则M∩N={x|0≤x<1}.
[答案] A
2.已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:
|
x |
1 |
2 |
3 |
|
f(x) |
2 |
3 |
1 |
|
x |
1 |
2 |
3 |
|
g(x) |
3 |
2 |
1 |
则方程g(f(x))=x的解集为( )
A.{1} B.{2}
C.{3} D.{∅}
[解析] 当x=1时,g(f(1))=g(2)=2,不合题意.
当x=2时,g(f(2))=g(3)=1,不合题意.
[答案] C
1.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是( )
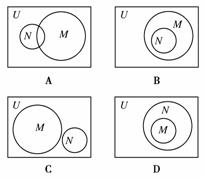
[解析] 由N={x|x2+x=0},得N={-1,0}.
∵M={-1,0,1},∴N⊆M,故选B.
[答案] B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com