20．(12分)某厂生产一种机器的固定成本(即固定投入)为0.5万元，但每生产100台，需要增加可变成本(即另增加投入)0.25万元．市场对此产品的年需求量为500台，销售的收入函数为R(x)＝5x－\f(x²,2)(0≤x≤5)，其中x是产品售出的数量(单位：百台)．

(1)把利润表示为年产量的函数；

(2)年产量是多少时，工厂所得利润最大？

(3)年产量是多少时，工厂才不亏本？

[解析]　(1)当x≤5时，产品能售出x百台；

当x＞5时，只能售出5百台，

故利润函数为L(x)＝R(x)－C(x)

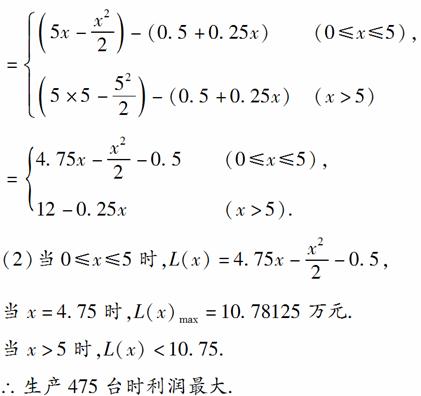
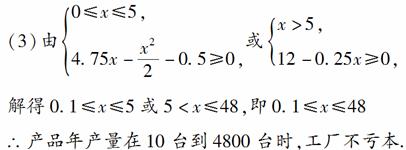
19．(12分)已知函数f(x)＝ax+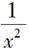 (x≠0，常数a∈R)．

(1)讨论函数f(x)的奇偶性，并说明理由；

(2)若函数f(x)在x∈[3，+∞)上为增函数， 求a的取值范围．

[解析]　(1)定义域(－∞，0)∪(0，+∞)，关于原点对称；

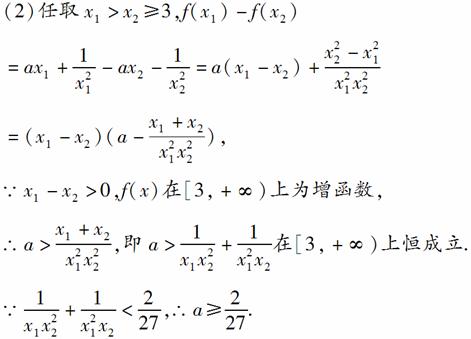
18．(12分)已知函数f(x)＝3^x，且f(a+2)＝18，g(x)＝3^ax－4^x的定义域为区间[－1,1]．

(1)求g(x)的解析式；

(2)判断g(x)的单调性．

[解析]　(1)∵f(a+2)＝18，f(x)＝3^x.

∴3^a+2＝18，即3^a＝2.

故g(x)＝(3^a)^x－4^x＝2^x－4^x，x∈[－1,1]．

(2)g(x)＝－(2^x)²+2^x＝－．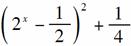

当x∈[－1,1]时，2^x∈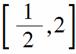．令t＝2^x，

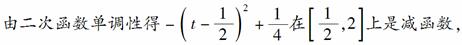
∴函数g(x)在[－1,1]上是减函数．

17．(10分)已知集合A＝{x|x²－4x－5≤0}，B＝{x|x²－2x－m<0}．

(1)当m＝3时，求A∩∁_RB；

(2)若A∩B＝{x|－1≤x<4}，求实数m的值．

[解析]　(1)A＝{x|x²－4x－5≤0}＝{x|－1≤x≤5}，

当m＝3时，B＝{x|－1<x<3}，

则∁_RB＝{x|x≤－1或x≥3}，

∴A∩∁_RB＝{x|x＝－1或3≤x≤5}．

(2)∵A∩B＝{x|－1≤x<4}，

∴x＝4是方程x²－2x－m＝0的一个根，

∴有4²－2×4－m＝0，解得m＝8，

此时B＝{x|－2<x<4}符合题意．

16．2009年12月18日，温家宝总理代表中国政府在哥本哈根气候变化会议上做出庄严承诺：2005年至2020年，中国单位国内生产总值二氧化碳排放强度下降40%，则2005年至2020年二氧化碳排放强度平均每年降低的百分数为________．

[解析]　设从2005年至2020年平均每年降低的百分数为x，则2020年的排放量为(1－x)¹⁵，即(1－x)¹⁵＝0.4，

解得x＝0.059.

∴2005年至2020年平均每年国内生产总值二氧化碳排放强度平均每年降低5.9%.

[答案]　5.9%

15．设函数f(x)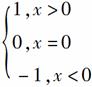＝，g(x)＝x²f(x－1)，则函数g(x)的递减区间是________．

[解析]　依题意有g(x)＝x²f(x－1)＝，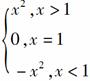

所以g(x)的递减区间是(0,1)．

[答案]　(0,1)

14．方程lg x²－lg(x+2)＝0的解集是________．

[解析]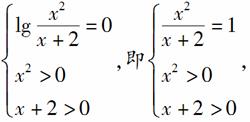

x²－x－2＝0，∴x＝2或x＝－1，

验证知x＝2与x＝－1均为根，

故解集为{－1,2}．

[答案]　{－1,2}

13．设U＝{n|n是小于9的正整数}，A＝{n∈U|n是奇数}，B＝{n∈U|n是3的倍数}，则∁_U(A∪B)＝________

[解析]　∵U＝{1,2,3,4,5,6,7,8}，A＝{1,3,5,7}，B＝{3,6}，∴A∪B＝{1,3,5,6,7}，∴∁_U(A∪B)＝{2,4,8}．

[答案]　{2,4,8}

12．定义在R上的偶函数f(x)满足：对任意的x₁，x₂∈(－∞，0](x₁≠x₂)，有(x₂－x₁)(f(x₂)－f(x₁))>0，则当n∈N^*时，有(　)

A．f(－n)<f(n－1)<f(n+1)

B．f(n－1)<f(－n)<f(n+1)

C．f(n+1)<f(－n)<f(n－1)

D．f(n+1)<f(n－1)<f(－n)

[解析]　对任意x₁，x₂∈(－∞，0](x₁≠x₂)，有(x₂－x₁)·(f(x₂)－f(x₁))>0，因此x₂－x₁和f(x₂)－f(x₁)同号，所以f(x)在(－∞，0]上是增函数．由于n∈N^*，且n+1>n>n－1，所以－n－1＜－n<－n+1＜0，即f(n+1)＝f(－n－1)<f(－n)<f(－n+1)＝f(n－1)．

[答案]　C

11．函数y＝f(x)的图象如图所示，则函数y＝log_0.5f(x)的图象大致是(　)

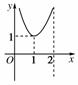
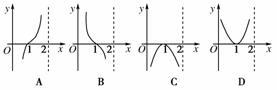
[解析]　由同增异减的单调性原则可得：当x∈(0,1)时

y=log0.5x为增函数，且y<0，当x∈(1,2)时y=log0.5x为减函数，且-1<y<0，分析各选项易知只有C符合上述条件．

当x=3时，g(f(3))=g(1)=3，符合题意．

[答案]　C