
13.已知直角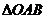 的直角顶点
的直角顶点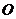 为原点,
为原点,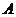 、
、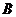 在抛物线
在抛物线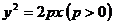 上,(1)分别求
上,(1)分别求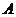 、
、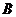 两点的横坐标之积,纵坐标之积;(2)直线
两点的横坐标之积,纵坐标之积;(2)直线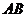 是否经过一个定点,若经过,求出该定点坐标,若不经过,说明理由;(3)求
是否经过一个定点,若经过,求出该定点坐标,若不经过,说明理由;(3)求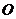 点在线段
点在线段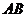 上的射影
上的射影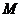 的轨迹方程
的轨迹方程
答案:(1)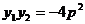 ;
;
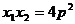 ;(2)直线
;(2)直线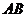 过定点
过定点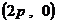
(3)点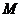 的轨迹方程为
的轨迹方程为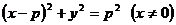
12.(07山东理21)(本小题满分12分)
已知椭圆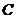 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在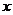 轴上,椭圆
轴上,椭圆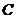 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为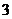 ,最小值为
,最小值为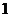 .
.
(Ⅰ)求椭圆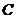 的标准方程;
的标准方程;
(Ⅱ)若直线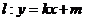 与椭圆
与椭圆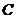 相交于
相交于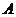 ,
,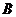 两点(
两点(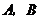 不是左右顶点),且以
不是左右顶点),且以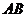 为直径的圆过椭圆
为直径的圆过椭圆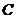 的右顶点,求证:直线
的右顶点,求证:直线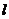 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
[标准答案](I)由题意设椭圆的标准方程为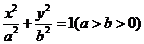
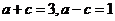 ,
,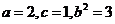
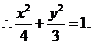
(II)设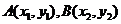 ,由
,由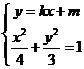 得
得
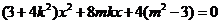 ,
,
 ,
,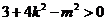 .
.
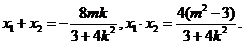
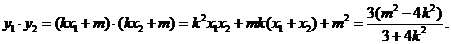
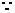 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点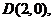
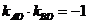 ,
,
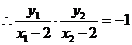 ,
,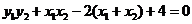 ,
,
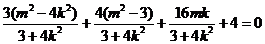 ,
,
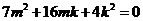 ,解得
,解得
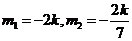 ,且满足
,且满足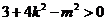 .
.
当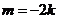 时,
时,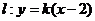 ,直线过定点
,直线过定点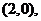 与已知矛盾;
与已知矛盾;
当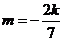 时,
时,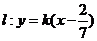 ,直线过定点
,直线过定点
综上可知,直线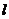 过定点,定点坐标为
过定点,定点坐标为
11.求直线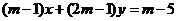 所经过的定点坐标.
所经过的定点坐标.
答案: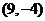
10. 已知焦点在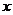 轴上的椭圆
轴上的椭圆
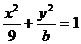 上存在两点
上存在两点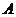 ,
,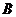 关于直线
关于直线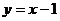 对称,求
对称,求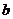 的取值范围.
的取值范围.
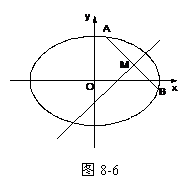
解法1:如图8-6,由题意可设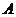 ,
,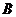 两点所在直线方程设为
两点所在直线方程设为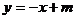 ,
,
代入椭圆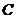 方程得
方程得
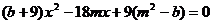 ,
,
 由
由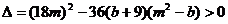 得
得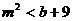 ,
,
设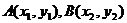 ,则
,则
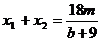 ,
,
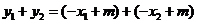
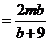 ,
,
所以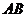 的中点
的中点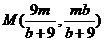 ,
,
因为点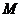 在直线
在直线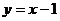 上,
上,
所以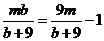 ,
,
解得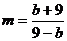 ,再将
,再将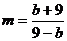 代入
代入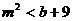 得
得
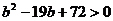 ,
,
解得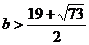 或
或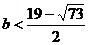 ,
,
因为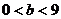 ,
,
所以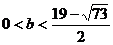 .
.
解法2:设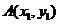 ,
,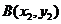 ,
,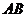 中点
中点 ,
,
由题意可得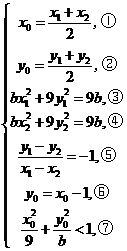
由③-④得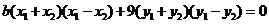 ,
,
将①②代入得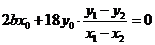 ,
,
将⑤代入结果得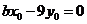 ,
,
再将⑥代入得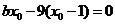 ,
,
解得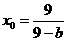 ,
,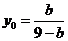 ,将
,将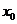 ,
,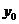 代入⑦得
代入⑦得
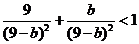 ,
,
化简得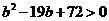 ,
,
解得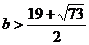 或
或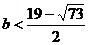 ,
,
因为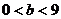 ,
,
所以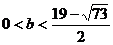 .
.
点评:对称问题应注意运用以下结论建立关系式:
(1)对称点的连线与对称轴垂直;
(2)对称点的中点在对称轴上;
(3)对称点所在的直线与曲线相交于两个不同的点.
本题在求参数范围时,解法1是利用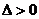 构造含参数
构造含参数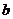 的不等式,解法2是利用
的不等式,解法2是利用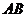 的中点
的中点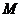 在椭圆内构造含参数的不等式.
在椭圆内构造含参数的不等式.
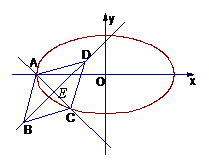
9.(2008北京理19)已知菱形ABCD的顶点A,C在椭圆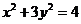 上,对角线BD所在直线的斜率为1.
上,对角线BD所在直线的斜率为1.
(Ⅰ)当直线BD过点(0,1)时,求直线AC的方程;
(Ⅱ)当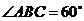 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.
 [答案]
[答案]
(Ⅰ)解法1:由题意得直线BD的方程为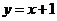 .
.
因为四边形ABCD为菱形,所以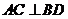 .
.
于是可设直线AC的方程为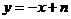 .
.
由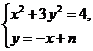 得
得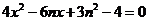 .
.
因为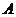 ,
,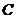 在椭圆上,
在椭圆上,
所以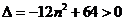 ,解得
,解得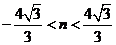 .
.
设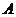 ,
,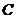 两点坐标分别
两点坐标分别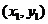 ,
,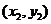 ,
,
则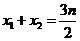 ,
,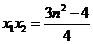 ,
,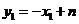 ,
,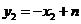 .
.
所以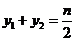 .
.
所以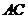 的中点
的中点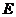 的坐标为(
的坐标为(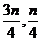 ).
).
由四边形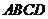 为菱形可知,点(
为菱形可知,点(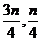 )在直线
)在直线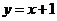 上,
上,
所以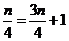 ,解得
,解得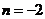 .
.
所以直线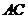 的方程为
的方程为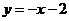 ,即
,即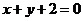 .
.
本题也可以由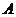 ,
,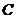 两点到直线
两点到直线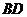 距离相等,得到
距离相等,得到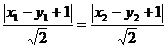 .
.
或者由点(0,1)到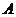 ,
,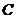 两点的距离相等,得到
两点的距离相等,得到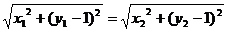 .
.
再由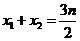 ,
,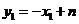 ,
,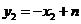 ,也能解得
,也能解得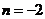 .
.
还可以由点(0,1)到直线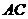 的距离等于点(0,1)与
的距离等于点(0,1)与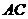 中点距离,
中点距离,
得到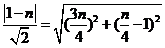 .解得
.解得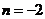 .
.
解法2设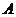 ,
,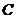 两点坐标分别为
两点坐标分别为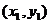 ,
,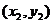 ,
,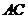 中点
中点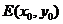
由题意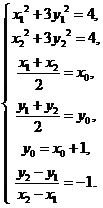
解得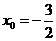 ,
,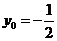 .
.
所以直线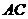 的方程为
的方程为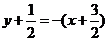 ,即
,即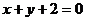 .(经检验,所求直线方程符合题意.)
.(经检验,所求直线方程符合题意.)
解法3设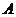 ,
,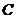 两点坐标分别为
两点坐标分别为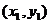 ,
,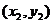 ,
,
因为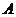 ,
,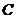 在椭圆上,所以
在椭圆上,所以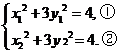
①-②得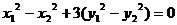 ,即
,即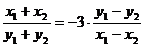 .
.
因为四边形 为菱形,所以
为菱形,所以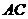
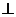
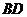 ,
,
所以直线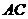 的斜率为
的斜率为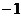 ,即
,即 .
.
所以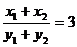 ,
,
设直线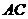 的方程为
的方程为 .
.
由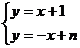 ,得到
,得到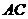 的中点
的中点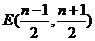 ,
,
于是有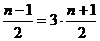 ,即
,即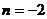 .
.
所以直线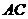 的方程为
的方程为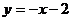 ,即
,即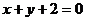 .
.
解法4设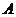 点坐标为
点坐标为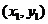 ,
,
因为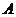 ,
,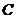 关于直线
关于直线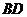 :
: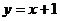 对称,
对称,
所以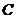 点坐标为
点坐标为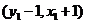 .
.
由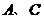 在椭圆上,得
在椭圆上,得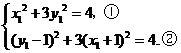 .
.
②-①并整理得到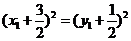 .
.
即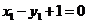 或
或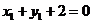 .
.
因为点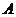 ,
,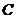 在直线上,且直线
在直线上,且直线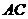 的斜率为
的斜率为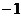 ,
,
所以点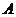 坐标
坐标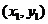 满足方程
满足方程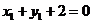 ,
,
因此直线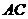 的方程为
的方程为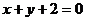 .
.
本题也可由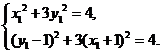 .
.
解得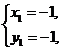 或
或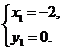
所以直线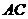 的方程为
的方程为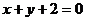 .
.
(Ⅱ)因为四边形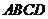 为菱形,且
为菱形,且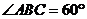 ,
,
所以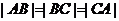 .
.
所以菱形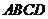 的面积
的面积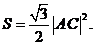
由(Ⅰ)可得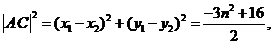

所以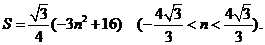
所以当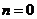 时,菱形
时,菱形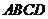 的面积取得最大值
的面积取得最大值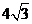 .
.
8.(2008北京19)已知△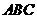 的顶点A,B在椭圆
的顶点A,B在椭圆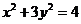 上,C在直线
上,C在直线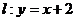 上,且AB//l.
上,且AB//l.
(Ⅰ)当AB边通过坐标原点O时,求AB的长及△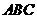 的面积;
的面积;
(Ⅱ)当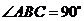 ,且斜边AC的长最大时,求AB所在直线的方程.
,且斜边AC的长最大时,求AB所在直线的方程.
[答案]
解:(Ⅰ)因为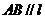 ,且AB边通过点(0,0),所以AB所在直线的方程为
,且AB边通过点(0,0),所以AB所在直线的方程为 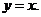
 设A,B两点坐标分别为
设A,B两点坐标分别为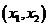 ,
,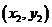 .
.
由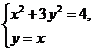 得
得 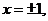
所以
又因为AB边上的高h等于原点到直线l的距离,
所以 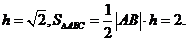
(Ⅱ)设AB所在直线的方程为 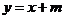 .
.
 由
由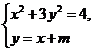 得
得 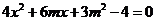 .
.
因为A,B在椭圆上,
所以 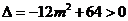 .
.
设A,B两点坐标分别为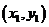 ,
,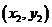 .
.
则 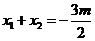 ,
,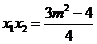 .
.
所以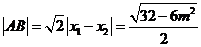 .
.
又因为BC的长等于点(0,m)到直线l的距离,即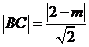 .
.
所以 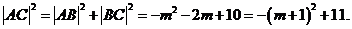
所以当 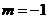 时,AC边最长.(这时
时,AC边最长.(这时 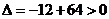 )
)
此时AB所在直线的方程为 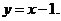
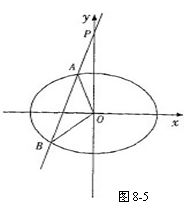
7.给定抛物线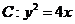 ,
,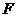 是
是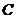 的焦点,过
的焦点,过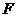 的直线
的直线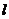 与
与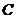 交于
交于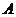 、
、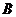 两点,记
两点,记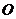 为坐标原点.
为坐标原点.
(1)
求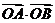 的值;
的值;
(2)
设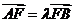 ,当三角形
,当三角形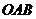 的面积
的面积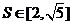 时,求
时,求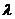 的取值范围.
的取值范围.
(1)解:设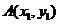 ,
,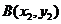 则
则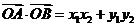 .
.
当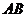 斜率不存在时,
斜率不存在时,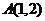 ,
,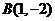 ,
,
所以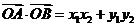
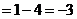 ;
;
当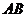 斜率存在时,设
斜率存在时,设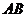 所在直线方程为
所在直线方程为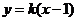
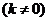 ,
,
由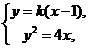 消去
消去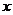 得
得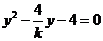 ,则
,则
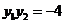 ,①
,①
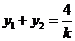 .②
.②
因为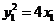 ,
,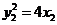 ,
,
所以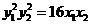 ,
,
所以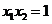 ,
,
因此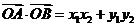
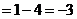 ,
,
综上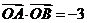 .
.
(2)解法1:由(1)知
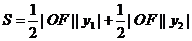
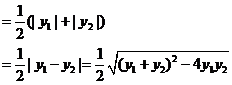
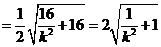 ,
,
因为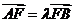 ,
,
所以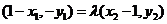 ,
,
所以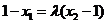 ,
,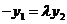 ,代入①②得
,代入①②得
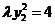 ,③
,③
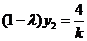 ,④,消去
,④,消去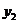 得
得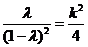 ,
,
所以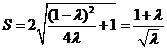 ,
,
由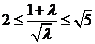 得
得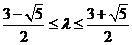 .
.
解法2:因为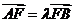 及点
及点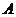 、
、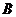 在抛物线
在抛物线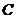 上,
上,
所以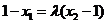 ,⑤
,⑤
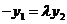 ,⑥
,⑥
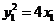 ,⑦
,⑦
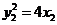 .⑧
.⑧
由⑥得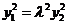 ,⑨
,⑨
⑦⑧代入⑨得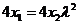 ,解得
,解得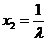 ,
,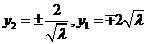 ,
,
所以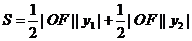
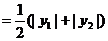
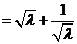 .以下同解法1.
.以下同解法1.
解法3:由题可知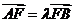 ,
, ,再根据抛物线定义可得
,再根据抛物线定义可得
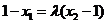 ,⑩
,⑩
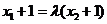 ,⑾
,⑾
由⑩⑾得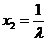 ,
,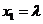 ,代入抛物线
,代入抛物线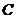 的方程得
的方程得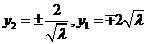 ,以下同解法2.
,以下同解法2.
 点评:本题是利用方程的思想、函数思想方法求参数
点评:本题是利用方程的思想、函数思想方法求参数 的范围.恰当运用图形的几何特征及抛物线的定义可简化运算量.
的范围.恰当运用图形的几何特征及抛物线的定义可简化运算量.
点评:求参数范围要注意寻找参数变化的根源,即所求的参数是随着哪个变量的变化而变化. 求参数范围主要方法有:(1)构造含参数的不等式通过解不等式求参数范围;(2)构造含参数的函数转化为求函数的值域或定义域;(3)利用曲线上的点的坐标的范围求参数的范围.本题主要思路是先寻找 与
与 的函数关系,再根据
的函数关系,再根据 范围求
范围求 范围.
范围.
6.已知点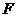 为椭圆
为椭圆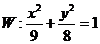 的右焦点,
点
的右焦点,
点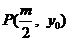 在椭圆W上,直线PF交椭圆W于点Q,且
在椭圆W上,直线PF交椭圆W于点Q,且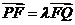 ,若
,若 ,求实数
,求实数 的范围.
的范围.
解法1:设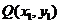 ,
,
因为 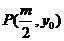 ,
,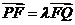 ,
,
所以 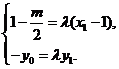 解得
解得
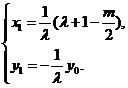
由点P、Q均在椭圆W上,
所以 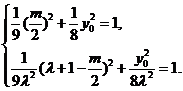
消去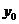 并整理,得
并整理,得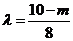 ,
,
因为 ,
,
所以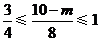 .
.
解得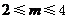 .
.
解法2:设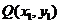 ,由题知
,由题知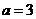 ,
,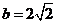 ,
,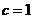 ,
,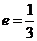 ,
,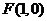 ,
,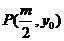 ,
,
因为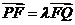 ,
,
所以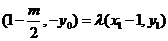 ,
,
于是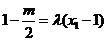 ,①
,①
由条件得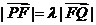 ,再由椭圆的第二定义得
,再由椭圆的第二定义得
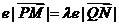 ,如图8-4.(点
,如图8-4.(点 ,
,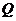 在右准线上的射影分别为
在右准线上的射影分别为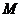 ,
,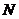 )
)
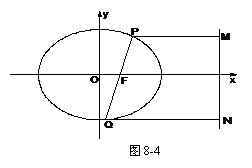 所以
所以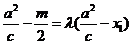 ,
,
即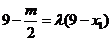 .②
.②
①+②得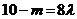 ,
,
于是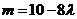 ,
,
因为 ,
,
所以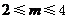 .
.
5.将圆O: 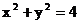 上各点的纵坐标变为原来的一半 (横坐标不变),
上各点的纵坐标变为原来的一半 (横坐标不变),
得到曲线C.
(1) 求C的方程;
(2)
设O为坐标原点, 过点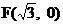 的直线l与C交于A、B两点, N为线段AB的中点,
的直线l与C交于A、B两点, N为线段AB的中点,
延长线段ON交C于点E.
求证: 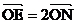 的充要条件是
的充要条件是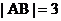 .
.
解: (1)设点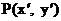 , 点M的坐标为
, 点M的坐标为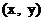 ,由题意可知
,由题意可知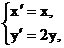 ………………(2分)
………………(2分)
又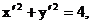 ∴
∴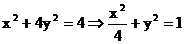 .
.
所以, 点M的轨迹C的方程为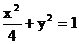 .………………(4分)
.………………(4分)
 (2)设点
(2)设点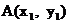 ,
,  ,
点N的坐标为
,
点N的坐标为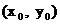 ,
,
㈠当直线l与x轴重合时, 线段AB的中点N就是原点O, 不合题意,舍去; ………………(5分)
㈡设直线l: 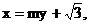
由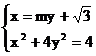 消去x,
消去x,
得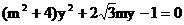 ………………①
………………①
∴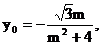 ………………(6分)
………………(6分)
∴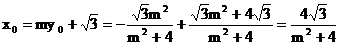 ,
,
∴点N的坐标为 .………………(8分)
.………………(8分)
①若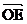
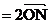 , 坐标为, 则点E的为
, 坐标为, 则点E的为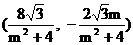 , 由点E在曲线C上,
, 由点E在曲线C上,
得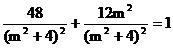 , 即
, 即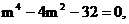 ∴
∴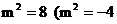 舍去).
舍去).
由方程①得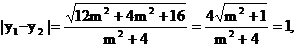
又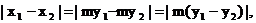
∴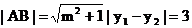 .………………(10分)
.………………(10分)
②若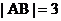 , 由①得
, 由①得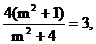 ∴
∴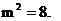
∴点N的坐标为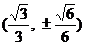 , 射线ON方程为:
, 射线ON方程为: 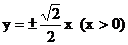 ,
,
由 解得
解得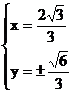 ∴点E的坐标为
∴点E的坐标为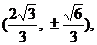
∴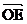
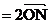 .
.
综上, 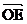
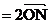 的充要条件是
的充要条件是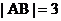 .
.
4.中心在原点,焦点在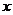 轴上的椭圆,离心率
轴上的椭圆,离心率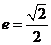 ,此椭圆与直线
,此椭圆与直线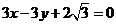 交于
交于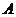 ,
,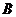 两点,且
两点,且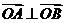 (其中
(其中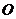 为坐标原点),求椭圆的方程.
为坐标原点),求椭圆的方程.
解:设椭圆方程为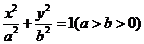 ,
,
因为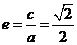 ,所以
,所以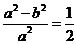 ,即
,即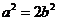 ,
,
所以椭圆方程化简为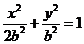 ,即为
,即为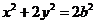 .
.
由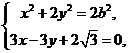 消去
消去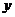 得
得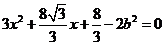 ,
,
设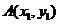 ,
,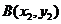 ,则
,则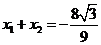 ,
,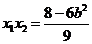 .
.
又因为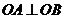 ,所以
,所以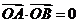 ,即
,即 ,
,
所以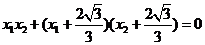 ,整理得
,整理得
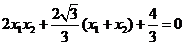 ,
,
所以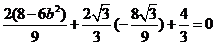 ,化简得
,化简得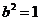 .
.
故所求椭圆方程为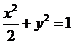 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com