
6.(2009·山东高考)集合A={0,2,a},B={1,a2}.若A∪B={0,1,2,4,16},则a的值为( )
A.0 B.1 C.2 D.4
解析:∵A∪B={0,1,2,a,a2},又A∪B={0,1,2,4,16},
∴{a,a2}={4,16},∴a=4.
答案:D
5.(2009·江苏高考)已知集合A={x|log2x≤2},B=(-∞,a),若A⊆B,则实数a的取值范围是(c,+∞),其中c= .
解析:A={x|0<x≤4},B=(-∞,a).
若A⊆B,则a>4.
即a的取值范围为(4,+∞),∴c=4.
答案:4
|
题组三 |
集合的基本运算 |
4.已知集合A={x|x2+x-6=0},B={x|mx+1=0},若B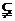 A,则实数m的取值集合是( )
A,则实数m的取值集合是( )
A.{-,0,} B.{0,1} C.{-,} D.{0}
解析:由x2+x-6=0得x=2或x=-3,
∴A={2,-3}.
又∵B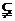 A,
A,
∴当m=0时,B=∅,满足条件;
当m≠0时,B={-},∴-=2或-=-3,
即m=-或m=.
答案:A
3.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是 ( )

 解析:∵M={-1,0,1},N={0,-1},∴N M.
解析:∵M={-1,0,1},N={0,-1},∴N M.
答案:B
2.已知集合A={a,b,2},B={2,b2,2a},则A∩B=A∪B,则a= .
解析:由A∩B=A∪B知A=B,又根据集合元素的互异性,所以有
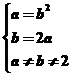
 或
或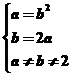 ,解得
,解得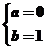 或
或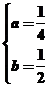

故a=0或
答案:0或
|
题组二 |
集合间的基本关系 |
1.(2009·广东高考)已知全集U=R,集合M={x|-2≤x-1≤2}和
N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所
示,则阴影部分所示的集合的元素共有 ( )
A.2个 B.3个 C.1个 D.无穷多个
解析:M={x|-1≤x≤3},N={x|x=2k-1,k∈N*},
∴M∩N={1,3}.
答案:A
4.(2010·四川南充)语言运用(2分)
一个顾客在酒吧里喝啤酒,他喝完第二杯之后,转身问酒吧的老板:“你们一周能卖掉多少桶啤酒?”老板得意洋洋地回答说:“35桶。”
顾客说:“我倒想出一个能使你每周卖掉70桶的办法。”
老板很惊讶,急忙问:“什么办法?”
顾客说:“这很简单,你只要将每个杯子里的啤酒装满就行。”
(1)老板急于讨教卖酒的办法,暴露了他什么心态?(1分)
答:
(2)顾客话中有何言外之意?(1分)
答:
[南充答案]语言运用(2分)
(1)暴露老板急于获取更多利益的心态。(1分)
(2)讽刺老板短斤少两,坑害顾客。(1分)(意近即可)
3.(2010·四川广安)下面说话最得体的一项是
A.“老师,”王东站起来,“这道题我还不懂,再给我讲一遍!”
B.小姚说:“李老师昨天病了,住在医院里。我们应该关怀关怀他,下午就去看看他。”
C.小明对深夜仍在大声喧闹的邻居说:“真不像话,这么晚了还在闹!”
D.张红在购书时,不慎将钱包丢在书店里,她连忙回去对中年女售书员说:“阿姨,我刚才买书时不小心将钱包丢了,您看见了吗?”
[广安答案]D
2.(2010·四川眉山)毕业前夕,我们班组织了一次“话说千古风流人物”综合性学习活动。在搜集整理资料中,我们发现,在我国古代历史长河中,曾经涌现出无数风流人物。文化名人灿若群星,英雄人物各领风骚。孔子“己所不欲,勿施于人”;陈涉仰天“王侯将相宁有种乎”;范仲淹登楼“先天下之忧而忧”;文天祥“留取丹心照汗青”;陶渊明“采菊东篱下,飞鸟相与还”。小明就此拟写了一幅对联,但下联不符合对联要求,请你修改或新对出下联。(2分)
上联:陶渊明安贫乐道东篱采菊 下联:狱中书心留取丹心文天祥
新创或修改为:
[眉山答案]此题为开放性试题,不设统一答案,强调基本符合对联知识。(2分)
修改:文天祥留取丹心狱中书志 新创:范仲淹忧乐天下登楼抒怀
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com