
22.(文)(本小题满分14分)已知m∈R,对p:x1和x2是方程x2-ax-2=0的两个根,不等 式|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立;q:函数f(x)=3x2+2mx+m+有两个不同的零点.求使“p且q”为真命题的实数m的取值范围.
解:由题设知x1+x2=a,x1x2=-2,
∴|x1-x2|==.
a∈[1,2]时,的最小值为3,要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只需|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+=0的判别式
Δ=4m2-12(m+)=4m2-12m-16>0,
得m<-1或m>4.
,综上,要使“p且q”为真命题,只需p真q真,
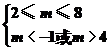
即 解得实数m的取值范围是(4,8].
(理)(本小题满分14分)设命题p:函数f(x)=lg(ax2-x+a)的定义域为R;命题q:不等式<1+ax对一切正实数均成立,如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
解:命题p为真命题⇔函数f(x)=lg(ax2-x+a)的定义域为R,
即ax2-x+a>0对任意实数x均成立,
得a=0时,-x>0的解集为R,不可能;
或
a<0时,ax2-x+解集显然不为R,
所以命题p为真命题⇔a>2.
命题q为真命题⇔-1<ax对一切正实数均成立,即a>=对一切正实数x均成立.
由于x>0,所以>1.
所以+1>2,所以<1.
所以,命题q为真命题⇔a≥1.
∵p或q为真命题,p且q为假命题,
∴p、q一真一假.
若p为真命题,q为假命题,无解;
若p为假命题,q为真命题,则1≤a≤2.
∴a的取值范围是[1,2].
21.(本小题满分12分)设全集是实数集R,A={x|2x2-7x+3≤0},
B={x|x2+a<0}.
(1)当a=-4时,求A∩B和A∪B;
(2)若(∁RA)∩B=B,求实数a的取值范围.
解:(1)∵A={x|≤x≤3},
当a=-4时,B={x|-2<x<2},
∴A∩B={x|≤x<2},A∪B={x|-2<x≤3}.
(2)∁RA={x|x<或x>3},
当(∁RA)∩B=B时,B⊆∁RA,
①当B=∅,即a≥0时,满足B⊆∁RA;
②当B≠∅,即a<0时,B={x|-<x<},要使B⊆∁RA,需≤,解得- ≤a<0.
综上可得,实数a的取值范围是a≥-.
19.(本小题满分12分)设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+(a2-5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
解:由x2-3x+2=0得x=1或x=2,
故集合A={1,2}.
(1)∵A∩B={2},∴2∈B,代入B中的方程,
得a2+4a+3=0⇒a=-1或a=-3;
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件;
综上,a的值为-1或-3;
(2)对于集合B,
Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B⊆A,
①当Δ<0,即a<-3时,B=∅满足条件;
②当Δ=0,即a=-3时,B={2},满足条件;
③当Δ>0,即a>-3时,B=A={1,2}才能满足条件,
则由根与系数的关系得

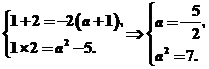
矛盾;
综上,a的取值范围是a≤-3.
 20.(本小题满分12分)(2010·盐城模拟)命题p:实数x满足x2-4ax+3a2<0,其中a<0,命题q:实数x满足x2-x-6≤0或x2+2x-8>0,且 p是 q的必要不充分条件,求a的取值范围.
20.(本小题满分12分)(2010·盐城模拟)命题p:实数x满足x2-4ax+3a2<0,其中a<0,命题q:实数x满足x2-x-6≤0或x2+2x-8>0,且 p是 q的必要不充分条件,求a的取值范围.
解:设A={x|x2-4ax+3a2<0(a<0)}={x|3a<x<a},
B={x|x2-x-6≤0或x2+2x-8<0}
={x|x2-x-6<0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}={x|x<-4或x≥-2}.
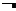
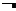 因为
p是 q的必要不充分条件,
因为
p是 q的必要不充分条件,
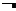
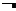
 所以 q⇒ p,且 p推不出
q而
所以 q⇒ p,且 p推不出
q而
 ∁RB={x|-4≤x<-2},∁RA={x|x≤3a,或x≥a}
∁RB={x|-4≤x<-2},∁RA={x|x≤3a,或x≥a}
所以{x|-4≤x<-2} {x|x≤3a或x≥a},
{x|x≤3a或x≥a},

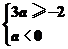 或
或
即-≤a<0或a≤-4.
18.(本小题满分12分)判断下列命题的真假.
(1)∀x∈R,都有x2-x+1>.
(2)∃α,β使cos(α-β)=cosα-cosβ.
(3)∀x,y∈N,都有x-y∈N.
(4)∃x0,y0∈Z,使得x0+y0=3.
解:(1)真命题,∵x2-x+1=(x-)2+≥>.
(2)真命题,如α=,β=,符合题意.
(3)假命题,例如x=1,y=5,但x-y=-4∉N.
(4)真命题,例如x0=0,y0=3符合题意.
17.(本小题满分12分)设集合A={-4,2a-1,a2},B={9,a-5,1-a},且A∩B={9},求实数a的值.
解:因为A∩B={9},所以9∈A.
若2a-1=9,则a=5,
此时A={-4,9,25},B={9,0,-4},A∩B={-4,9},与已知矛盾(舍去).
若a2=9,则a=±3.
当a=3时,A={-4,5,9},B={-2,-2,9},与集合中元素的互异性矛盾(舍去);
当a=-3时,A={-4,-7,9},B={-8,4,9},符合题意.
综上所述,a=-3.
16.(文)下列结论:
 ①若命题p:∃x∈R,tanx=1;命题q:∀x∈R,x2-x+1>0.则命题“p∧ q”是假命题;
①若命题p:∃x∈R,tanx=1;命题q:∀x∈R,x2-x+1>0.则命题“p∧ q”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.其中正确结论的序号为 (把你认为正确结论的序号都填上).
 解析:①中命题p为真命题,命题q为真命题,所以p∧ q为假命题,故①正确;
解析:①中命题p为真命题,命题q为真命题,所以p∧ q为假命题,故①正确;
②当b=a=0时,有l1⊥l2,故②不正确;
③正确,所以正确结论的序号为①③.
答案:①③
(理)给出下列四个命题:①∃α>β,使得tanα<tanβ;
②若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈(,),则f(sinθ)>f(cosθ);
③在△ABC中,“A>”是“sinA>”的充要条件;
④若函数y=f(x)的图象在点M(1,f(1))处的切线方程是y=x+2,则f(1)+f′(1)=3.其中所有正确命题的序号是 .
解析:①存在α=>β=,使tan=tan<tan,①正确;
②f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,则在[0,1]上是减函数,θ∈(,),1>sinθ>cosθ>0,
∴f(sinθ)<f(cosθ),②错误;
③在△ABC中,A>,则0<sinA≤1.
sinA>,则>A>,所以“A>”是“sinA>”的既必要不充分条件,③错误;
④函数y=f(x)在点M(1,f(1))处的切线斜率为f′(1)=,M(1,f(1))是曲线上的点也是切线上的点,x=1时,f(1)=,∴f(1)+f′(1)=3,④正确.
答案:①④
15.已知集合A={x|-1≤x≤1},B={x|1-a≤x≤2a-1},若B⊇A,那么a的取值范围是 .
 解析:由数轴知,
解析:由数轴知,

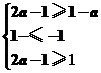 即
即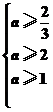
故a≥2.
答案:a≥2
14.已知m、n是不同的直线,α、β是不重合的平面.
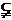 命题p:若α∥β,m?α,n?β,则m∥n;
命题p:若α∥β,m?α,n?β,则m∥n;
命题q:若m⊥α,n⊥β,m∥n,则α∥β;
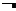
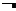 下面的命题中,①p或q;②p且q;③p或
下面的命题中,①p或q;②p且q;③p或
 q;④ p且q.
q;④ p且q.
真命题的序号是 (写出所有真命题的序号).
解析:∵命题p是假命题,命题q是真命题.
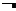
 ∴ p是真命题, q是假命题,
∴ p是真命题, q是假命题,
∴p或q是真命题,p且q是假命题,
 p或
q是假命题, p且q是真命题.
p或
q是假命题, p且q是真命题.
答案:①④
13.令p(x):ax2+2x+1>0,若对∀x∈R,p(x)是真命题,则实数a的取值范围是 .
解析:对∀x∈R,p(x)是真命题,就是不等式ax2+2x+1>0对一切x∈R恒成立.
 (1)若a=0,不等式化为2x+1>0,不能恒成立;
(1)若a=0,不等式化为2x+1>0,不能恒成立;
(2)若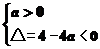 解得a>1;
解得a>1;
(3)若a<0,不等式显然不能恒成立.
综上所述,实数a的取值范围是a>1.
答案:a>1
12.(文)已知P={x|x2-4x+3≤0},Q={x|y=+},则“x∈P”是“x∈Q”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:解集合P中的不等式x2-4x+3≤0可得1≤x≤3,集合Q中的x满足,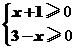 ,解之得-1≤x≤3,所以满足集合P的x均满足集合Q,反之,则不成立.
,解之得-1≤x≤3,所以满足集合P的x均满足集合Q,反之,则不成立.
答案:A
(理)设集合A={x|<0},B={x|x2-4x<0},那么“m∈A”是“m∈B”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:∵A={x|0<x<1},B={x|0<x<4},
 ∴A?B,∴“m∈A”是“m∈B”的充分不必要条件.
∴A?B,∴“m∈A”是“m∈B”的充分不必要条件.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com