
6.函数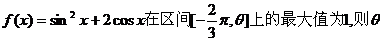 的值是( D )
的值是( D )
A.0 B.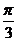 C.
C.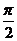 D.-
D.-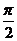
5.若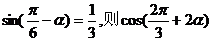 的值为 (D )
的值为 (D )
A. B.-
B.- C.
C.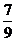 D.-
D.-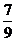
4.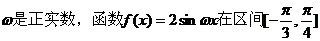 上递增,那么
( A )
上递增,那么
( A )
A.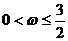 B.
B.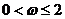
C.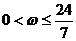 D.
D.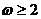
3.△ABC中,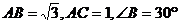 ,则△ABC的面积等于( C ).
,则△ABC的面积等于( C ).
A.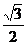 B.
B.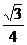 C.
C.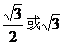 D.
D.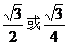
2.设函数f(x)=sin(ω+φ)(ω>0,-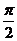 ),有下列论断:
),有下列论断:
①f(x)的图象关于直线x=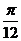 对称; ②f(x)的图象关于(
对称; ②f(x)的图象关于( )对称;
)对称;
③f(x)的最小正周期为π; ④在区间[-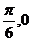 ]上,f(x)为增函数.
]上,f(x)为增函数.
以其中的两个论断为条件,剩下的两个论断为结论,写出你认为正确的一个命题:若_____②④或②③______,则_______①④________.(填序号即可)
11.对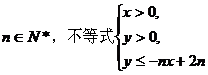 所表示的平面区域为Dn,把Dn内的整点(横
所表示的平面区域为Dn,把Dn内的整点(横
坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列: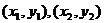 ,
,
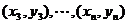 .
.
(Ⅰ)求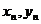 ;
;
(Ⅱ)数列{an}满足a1=x1,且
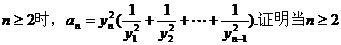 时,
时,
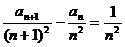 .
.
(Ⅰ)解: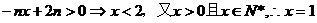
故Dn内的整点都落在直线x=1上,且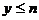 ,故Dn内的整点按其到原点的距离从近到远排成的点列为(1,1),(1,2),…,(1,n),∴
,故Dn内的整点按其到原点的距离从近到远排成的点列为(1,1),(1,2),…,(1,n),∴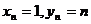
(Ⅱ)证明:当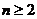 时,
时,
由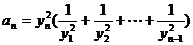 ,得
,得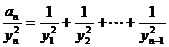
即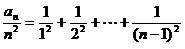 …………①
…………①
∴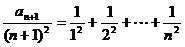 …………②
…………②
②式减①式,得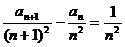 .
.
高考动车组2
三角函数1
l 同角三角函数的基本关系式
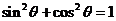 ,
, =
=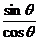 ,
,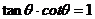 .
.
l 和角与差角公式
 ;
;
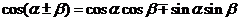 ;
;
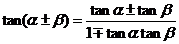 .
.
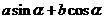 =
=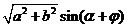 (辅助角
(辅助角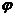 所在象限由点
所在象限由点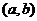 的象限决定,
的象限决定, ).
).
l 二倍角公式
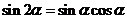 .
.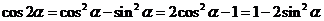 .
.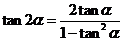
l 三角函数的周期公式
函数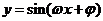 ,x∈R及函数
,x∈R及函数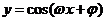 的周期
的周期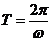 ;函数
;函数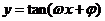 的周期
的周期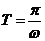 .
.
例1.已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB=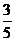 .
.
(1)若b=4,求sinA的值; (2) 若△ABC的面积S△ABC=4,求b,c的值.
解:(1) ∵cosB=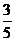 >0,且0<B<π,∴sinB=
>0,且0<B<π,∴sinB= .
.
由正弦定理得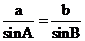 ,
,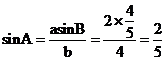 .
.
(2) ∵S△ABC=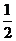 acsinB=4,∴
acsinB=4,∴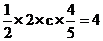 , ∴c=5.
, ∴c=5.
由余弦定理得b2=a2+c2-2accosB,
∴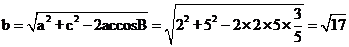 .
.
例2.在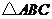 中,已知
中,已知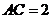 ,
,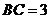 ,
,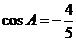 .
.
(1)求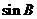 的值;
的值;
(2)求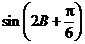 的值.
的值.
解:(1)由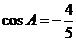 可得
可得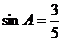 所以由正弦定理可得
所以由正弦定理可得 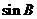 =
=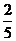
(2)由已知可知A为钝角,故得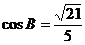
从而  ,
,
所以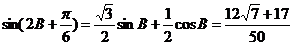
例3.给出下面的三个命题:①函数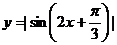 的最小正周期是
的最小正周期是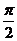 ②函数
②函数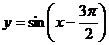 在区间
在区间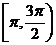 上单调递增③
上单调递增③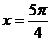 是函数
是函数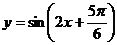 的图象的一条对称轴。其中正确的命题个数( C )
的图象的一条对称轴。其中正确的命题个数( C )
A.0 B.1 C.2 D.3
例3.已知函数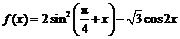 ,
, .
.
(1)求 的最大值和最小值;
的最大值和最小值;
(2)若不等式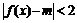 在
在 上恒成立,求实数
上恒成立,求实数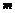 的取值范围
的取值范围
解: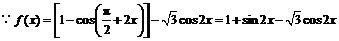
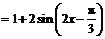 . 又
. 又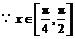 ,
,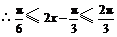 ,即
,即 ,
,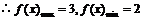 .
.
(2)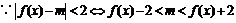 ,
, ,
,
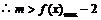 且
且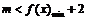 ,
,
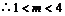 ,即
,即 的取值范围是
的取值范围是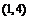 .
.
例4.已知:函数 .
.
(1)求函数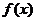 的最小正周期和值域;
的最小正周期和值域;
(2)若函数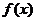 的图象过点
的图象过点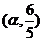 ,
,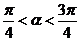 .求
.求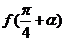 的值
的值

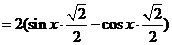
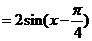
∴函数的最小正周期为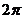 ,值域为
,值域为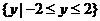 。
。
(2)解:依题意得: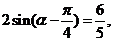
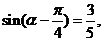
∵ ∴
∴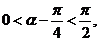
∴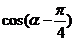 =
=
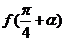 =
=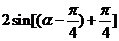
∵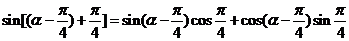 =
=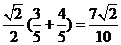
∴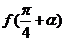 =
=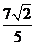
作业:1.定义一种运算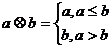 ,令
,令
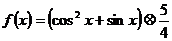 ,且
,且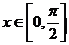 ,则函数
,则函数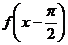 的最大值是 ( A) ( )
的最大值是 ( A) ( )
A.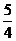 B.1 C.
B.1 C.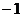 D.
D.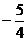
10.函数f(x)=a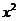 +bx +c (a
+bx +c (a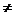 0) 的图象关于直线x= -
0) 的图象关于直线x= -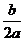 对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程 m[f(x)]
对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程 m[f(x)] 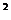 +nf(x) +p=0的解集都不可能是( D)
+nf(x) +p=0的解集都不可能是( D)
A. 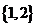 B
B
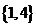 C
C
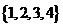 D
D 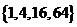
9.若曲线y=f(x)上存在三点A、B、C,使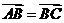 ,则称点曲线有“中位点”,下列曲线:①y=cosx, ②
,则称点曲线有“中位点”,下列曲线:①y=cosx, ②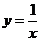 ,③
,③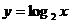 ,④y=cosx+x2,⑤
,④y=cosx+x2,⑤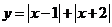 ,有“中位点”的有
(写出所有满足要求的序号)
①⑤
,有“中位点”的有
(写出所有满足要求的序号)
①⑤
8.(2009厦门二中)已知命题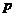 :
: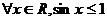 ,则………( )
,则………( )
A.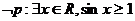 B.
B.

C.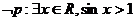 D.
D. 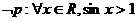
C
7.若集合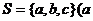 、b、
、b、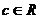 )中三个元素为边可构成一个三角形,那么该三角形一定不可能是( )
)中三个元素为边可构成一个三角形,那么该三角形一定不可能是( )
A.锐角三角形 B.等腰三角形 C.钝角三角形 D.直角三角
B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com