
第一节:单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
21.I wonder what it feels like to be one of _ ___ really rich. The Brows already have Rolls Royce and now they are buying _____ third.
A. the; the B.不填; a C. the; a D.不填; the
14.(本小题满分13分)
已知函数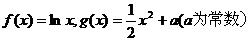 ,若直线
,若直线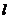 与
与 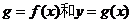 的图象都相切,且
的图象都相切,且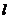 与
与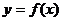 的图象相切于定点
的图象相切于定点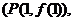
(1)求直线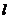 的方程及a的值;
的方程及a的值;
(2)当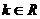 时,讨论关于x的方程
时,讨论关于x的方程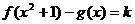 的实数解的个数.
的实数解的个数.
[解](1)∵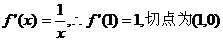 2分
2分
∴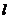 的解析式为
的解析式为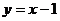 .
3分
.
3分
又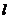 与
与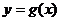 相切,
相切,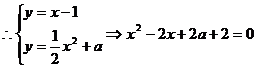 4分
4分
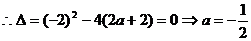 6分
6分
(2)令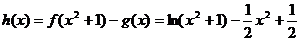
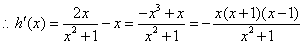 8分
8分
令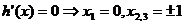 .
.
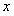 |
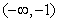 |
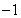 |
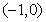 |
0 |
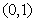 |
1 |
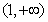 |
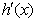 |
+ |
0 |
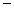 |
|
+ |
|
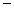 |
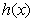 |
↗ |
极大值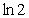 |
↘ |
极小值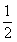 |
↗ |
极大值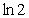 |
↘ |
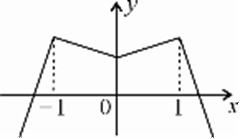 10分
10分
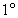
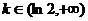 时,方程无解.
时,方程无解.
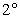 当
当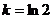 时,方程有2解.
时,方程有2解.
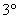 当
当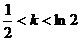 ,方程有4解.
,方程有4解.
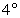 当
当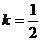 时,方程有3解.
时,方程有3解.
 当
当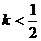 时,方程有2解.
13分
时,方程有2解.
13分
13.(本小题满分13分)
某化工企业生产某种产品,生产每件产品的成本为3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11 – x)2万件;若该企业所生产的产品能全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a (1≤a≤3).
(Ⅰ)求该企业正常生产一年的利润L (x)与出厂价x的函数关系式;


(Ⅱ)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
[解](Ⅰ)依题意,L (x) = (x – 3 ) (11 – x)2 – a (11 – x)2
= (x – 3 – a) (11 – x)2,x∈[7,10]. ………………5分
(Ⅱ)因为L′(x) = (11 – x)2 – 2 (x – 3 – a) (11 – x) = (11 – x ) (11 – x – 2x + 6 + 2a)
= (11 – x )(17 + 2a – 3x).
由L′(x) = 0,得x = 11 [7,10]或x
=
[7,10]或x
= 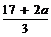 . ………………7分
. ………………7分
∵1≤a≤3,∴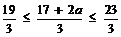 .
.
在x = 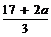 的两侧L′(x)由正变负, ……………………8分
的两侧L′(x)由正变负, ……………………8分 

故①当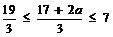 ,即1≤a≤2时,L′(x)在[7,10]上恒为负,∴L
(x)在[7,10]上为减函数.
,即1≤a≤2时,L′(x)在[7,10]上恒为负,∴L
(x)在[7,10]上为减函数.
∴[L (x)]max = L (7) = 16 (4 – a). ………………………………10分
②当7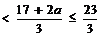 ,即2<a≤3时,
,即2<a≤3时,

 [L (x)]max = L
[L (x)]max = L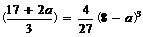 ……12分
……12分
即1≤a≤2时,则当每件产品出厂价为7元时,年利润最大,为16 (4 – a)万元.当2<a≤3时,则每件产品出厂价为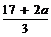 元时,年利润最大,为
元时,年利润最大,为 (8 – a)3万元. …………13分
(8 – a)3万元. …………13分
12.(本小题满分12分) 
已知y = f (x)是定义在[–1,1]上的奇函数,x∈[0,1]时,f (x) =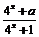 .
.
(1)求x∈[–1,0)时,y = f (x)解析式,并求y = f (x)在[0,1]上的最大值.
(2)解不等式f (x)>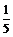 .
.
[解析](1)∵y = f (x)为奇函数 ∴f (0) =
0 ∴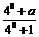 =0 ∴a = –1 ……2分
=0 ∴a = –1 ……2分
设x∈[–1,0)则–x∈(0,1] ∴f (x) = –f (–x) =–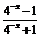 =–
=–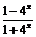 ……5分
……5分
x∈[0,1]时,f (x) = 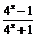 =
=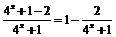
∴y = f (x)在[0,1]上为增函数.∴f(x)max = f (1) =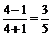 . ……7分
. ……7分
(2)∵y = f (x)为奇函数
∴x∈[–1,0)时,y = f (x)为单调递增函数 

∴x∈[–1,0)时,f (x) < f (0) =0 ……9分
由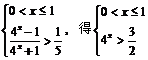 ∴
∴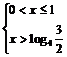 ∴
∴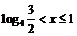 .……12分
.……12分
11.(本小题满分12分)
已知函数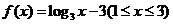 ,设
,设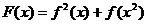

.(1)求F(x)的最大值及最小值. 
(2) 已知条件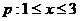 ,条件
,条件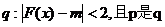 的充分条件,求实数m的取值范围.
的充分条件,求实数m的取值范围. 


[解](1)∵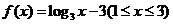

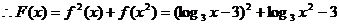

=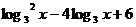 2分
2分
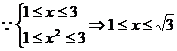 4分
4分
令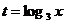 ,则
,则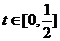 ,
,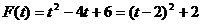 5分
5分
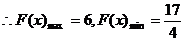 .
6分
.
6分
(2)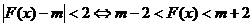 8分
8分
∵ p是q的充分条件,
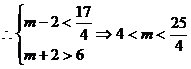 11分
11分
∴m的取值范围是 12分
12分
10. 将全体正整数排成一个三角形数阵:
|






根据以上排列规律,数阵中第n(n≥3)行的从左向右的第3个数是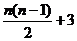

[解析] 因为第n行共有n个数,所以前n-1行共有1+2+…+(n-1)=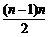 个数,则第n行(n≥3)从左向右的第3个数为
个数,则第n行(n≥3)从左向右的第3个数为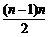 +3.
+3.
9. 某地区为了解70~80岁老人的日睡眠时间(单位:h),现随机地选出50名做调查,下表是日睡眠时间频率分布表:
某地区为了解70~80岁老人的日睡眠时间(单位:h),现随机地选出50名做调查,下表是日睡眠时间频率分布表:

序号 (i) |
分组 (睡眠时间) |
组中值 (Gi) |
频数 (人数) |
频率 (Fi) |
|
1 |
[4,5) |
4.5 |
6 |
0.12 |
|
2 |
[5,6) |
5.5 |
10 |
0.2 |
|
3 |
[6,7) |
6.5 |
20 |
0.4 |
|
4 |
[7,8) |
7.5 |
10 |
0.2 |
|
5 |
[8,9] |
8.5 |
4 |
0.08 |

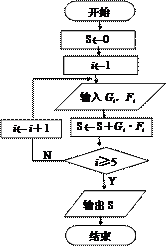
在上述统计数据的分析中,一部分计算见算法流程图,则输出的S的值为 6.42 .
[解析]S=4.5×0.12+5.5×0.2+6.5×0.4+7.5×0.2+8.5×0.08=6.42.
8. 设x,y,z为正实数,x-2y+3z=0,则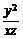 的最小值是3.
的最小值是3.
[解析]∵x,z>0,∴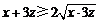 ,∵x-2y+3z=0,∴
,∵x-2y+3z=0,∴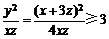

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com