2．如果你发现自己遇事容易急躁、冲动，可以选择下列哪种运动项目(　　 ) (2分)

　 　　 A．乒乓球　　　　　　　　　 B．围棋　　　　　　　　　　　 C．扑克　　　　　　　　　　　 D．跳绳

1．融音乐、舞蹈和体育为一体的竞技体育项目，具有较高的观赏价值。优美动听的音乐，

风格各异的舞蹈动作，眼花缭乱的抛接和空中翻腾，使人得到高雅、优美与惊险相结合

的艺术享受。下面是由音乐伴奏的竞技体育比赛项目是(　　 )

　 　　 A．街舞　　　　　　　　　　　 B．健身操　　　　　　　　　 C．花样滑水　　　　　　　 D．广播体操

12．(16分)通过研究学生的学习行为，专家发现，学生的注意力随着老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增；中间有一段时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，设f(t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大，表明学生注意力越集中)，经过试验分析得知：

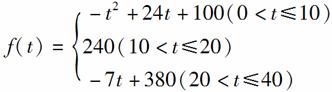
(1)讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

(2)讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？

(3)一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？

[解析]　(1)当0＜t≤10时，

f(t)＝－t²+24t+100＝－(t－12)²+244是增函数，且f(10)＝240.

当20＜t≤40时，f(t)＝－7t+380是减函数，且f(20)＝240.

所以，讲课开始后10分钟时，学生的注意力最集中，能持续10分钟．

(2)f(5)＝195，f(25)＝205，

所以讲课开始后25分钟时，学生的注意力比讲课开始后5分钟更集中．

(3)当0＜t≤10时，令f(t)＝－t²+24t+100＝180，则t＝4；

当20＜t≤40时，令f(t)＝－7t+380＝180，则t≈28.57，

则学生注意力在180以上所持续的时间为28.57－4

＝24.57＞24.

所以，经过适当安排，老师可以在学生达到所需要的状态下讲授完这道题目．

11．(15分)某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图)．

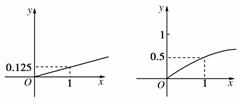
(1)分别写出两种产品的收益与投资的函数关系；

(2)该家庭现有20万元资金，全部用于理财投资，问：怎样分配资金能使投资获得最大收益，其最大收益为多少万元？

10．(15分)某市居民自来水收费标准如下：每户每月用水不超过4吨时每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元，已知甲、乙两户该月用水量分别为5x,3x(吨)．

(1)求y关于x的函数；

(2)若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量和水费．

[解析]　(1)当甲的用水量不超过4吨时，即5x≤4，乙的用水量也不超过4吨，y＝1.8(5x+3x)＝14.4x；

当甲的用水量超过4吨，乙的用水量不超过4吨，即3x≤4且5x>4时，

y＝4×1.8+3x×1.8+3(5x－4)＝20.4x－4.8.

当乙的用水量超过4吨，即3x>4时，

y＝2×4×1.8+3×[(3x－4)+(5x－4)]＝24x－9.6.

所以甲户用水量为5x＝7.5吨，

付费S₁＝4×1.8+3.5×3＝17.70(元)；

乙户用水量为3x＝4.5吨，

付费S₂＝4×1.8+0.5×3＝8.70(元)．

9.

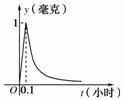
2009年10月，H1N1病毒，再次传播，为了预防流感，某学校对教室用药熏消毒法进行消毒．已知药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比；药物释放完毕后，y与t的函数关系式为y=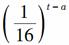 (a为常数)，如图所示．根据图中提供的信息，回答下列问题：

(1)从药物释放开始，每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为________；

(2)据测定：当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过________小时后，学生才能回到教室．

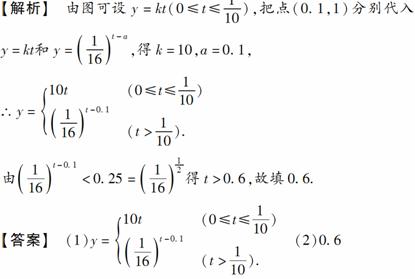
8．2009年初，南京、杭州两市相继发生严重交通事故，公安部和交通部联合出台一些法规，我们知道一个人喝了少量酒后，血液中的酒精含量迅速上升到0.3 mg/ml，在停止喝酒后，血液中的酒精含量以每小时25%的速度减少，为了保障交通安全，某地根据《道路交通安全法》规定：驾驶员血液中的酒精含量不得超过0.09 mg/ml，那么，一个喝了少量酒后的驾驶员，至少经过________小时，才能开车？(精确到1小时)

[解析]　设x小时后，血液中的酒精含量不超过0.09 mg/ml，则有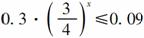≤0.09，即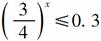，估算或取对数计算得5小时后，可以开车．

[答案]　5

7．某企业年初有资金100万元，若该企业经过有效经营能使每年资金平均增长50%，但每年年底要扣除消费基金x万元，余下投入再生产，为实现3年后资金达290万元(扣除消费基金后)，则x＝________.

[解析]　第一年后剩余资金为150－x；

第二年剩余资金为(150－x)×1.5－x；

第三年剩余资金为(225－2.5x)×1.5－x＝290⇒x＝10.

[答案]　10

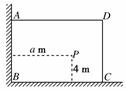
6．如图，有一直角墙角，两边的长度足够长，在P处有一棵树与两墙的距离分别为a m(0<a<12)、4 m，不考虑树的粗细．现在想用16 m长的篱笆，借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的面积为S m²，S的最大值为f(a)，若将这颗树围在花圃内，则函数u＝f(a)的图象大致是(　)

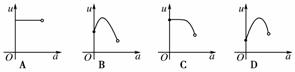
[解析]　先从确定花圃的最大面积入手，注意由于要将树围在里面，则其边长有限制，在此条件下确定花圃的最大面积，可转化为二次函数区间最值，最终整理成关于a的一个分

段函数．据题意设BC＝x，则DC＝16－x，要使树围在花圃内，需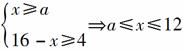，此时花圃的面积f(x)＝x(16－x)

＝－(x－8)²+64(a≤x≤12)，当8<a≤12时，有S＝f(a)＝－a²+16a，当0<a≤8时有S＝f(8)＝64，综上所述可得：S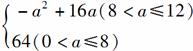＝，作出图形易知C选项正确．

[答案]　C

5．如图，点P在边长为1的正方形ABCD上运动，设点M为CD的中点，当点P沿A→B→C→M运动时，点P经过的路程设为x，△APM面积设为y，则函数y＝f(x)的图象只可能是下图中的(　)

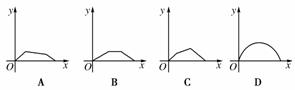
[解析]　据题意可得

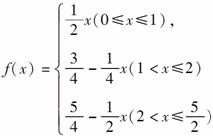
，易知只有A选项符合条件．

[答案]　A