5．已知映射f:A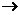B,其中集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中元素在映射f下的象,且对任意的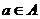,在B中和它对应的元素是,则集合B中元素的个数是(　 )

A．4 　　　 B．5　　　 C．6 　　　 D．7

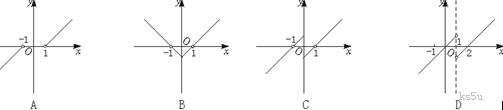
4．奇函数y=f(x)(x≠0)，当x∈(0，+∞)时，f(x)=x－1，则函数f(x－1)的图象为　 ( 　 )

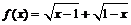3．已知函数(1),　 (2),(3)

(4)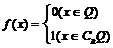,其中是偶函数的有(　 )个

A．1　 　　　B．2 　　　C．3 　　　 D．4　

2．函数是(　 )

A． 非奇非偶函数　 B．既不是奇函数,又不是偶函数奇函数　　 C． 偶函数　　 D． 奇函数

1．已知函数f(x)=2x2-mx+3，当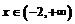时是增函数，当时是减函数，则f(1)等于　　　　　　　　　　　　　　　　　　　　　　　 (　 )

　A．-3　　　B．13 　　　C．7　 　　D．含有m的变量 　　

14．在边长为2的正方形ABCD的边上有动点M，从点B开始，沿折线BCDA向A点运动，设M点运动的距离为x，△ABM的面积为S．

(1)求函数S=的解析式、定义域和值域；

(2)求f[f(3)]的值．

必修1　　　　　　　　　　 第2章　 函数概念与基本初等函数Ⅰ

§2.1.2 函数的简单性质

重难点：领会函数单调性的实质，明确单调性是一个局部概念，并能利用函数单调性的定义证明具体函数的单调性，领会函数最值的实质，明确它是一个整体概念，学会利用函数的单调性求最值；函数奇偶性概念及函数奇偶性的判定；函数奇偶性与单调性的综合应用和抽象函数的奇偶性、单调性的理解和应用；了解映射概念的理解并能区别函数和映射．

考纲要求：①理解函数的单调性、最大(小)值及其几何意义；结合具体函数，了解函数奇偶性的含义；并了解映射的概念；

②会运用函数图像理解和研究函数的性质．

经典例题：定义在区间(－∞，+∞)上的奇函数f(x)为增函数，偶函数g(x)在［0，+∞ )上图象与f(x)的图象重合.设a＞b＞0，给出下列不等式，其中成立的是

f(b)－f(－a)＞g(a)－g(－b)　 ②f(b)－f(－a)＜g(a)－g(－b)

　　③f(a)－f(－b)＞g(b)－g(－a)　 　④f(a)－f(－b)＜g(b)－g(－a)

A．①④　　　　　 　　　　　　 B．②③　　　　　　　　　　　 C．①③　　　　　　　　　　　 D．②④

当堂练习：

13．已知f(x)=x2+4x+3，求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t)．

12．求函数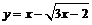的值域．

11． 求下列函数的定义域 ： (1)　　 　　(2)　

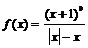
10．函数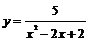的值域是　　　　　 　．