
3.如图,曲线c1, c2分别是函数y=xm和y=xn在第一象限的图象,
那么一定有( )
A.n<m<0 B.m<n<0 C.m>n>0 D.n>m>0
3.函数y=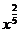 的单调递减区间为( )
的单调递减区间为( )
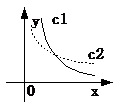 A.(-∞,1) B.(-∞,0) C.[0,+∞ ] D.(-∞,+∞)
A.(-∞,1) B.(-∞,0) C.[0,+∞ ] D.(-∞,+∞)
1.函数y=(x2-2x)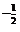 的定义域是( )
的定义域是( )
A.{x|x≠0或x≠2} B.(-∞,0)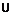 (2,+∞) C.(-∞,0)
(2,+∞) C.(-∞,0)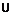 [2,+∞ ) D.(0,2)
[2,+∞ ) D.(0,2)
14.已知函数f(x)=x2-1(x≥1)的图象是C1,函数y=g(x)的图象C2与C1关于直线y=x对称.
(1)求函数y=g(x)的解析式及定义域M;
(2)对于函数y=h(x),如果存在一个正的常数a,使得定义域A内的任意两个不等的值x1,x2都有|h(x1)-h(x2)|≤a|x1-x2|成立,则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明:y=g(x)是M上的利普希茨Ⅰ类函数.
 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.4幂函数
重难点:掌握常见幂函数的概念、图象和性质,能利用幂函数的单调性比较两个幂值的大小.
考纲要求:①了解幂函数的概念;
②结合函数 的图像,了解他们的变化情况.
的图像,了解他们的变化情况.
经典例题:比较下列各组数的大小:
(1)1.5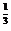 ,1.7
,1.7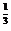 ,1; (2)(-
,1; (2)(-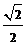 )
)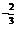 ,(-
,(-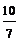 )
)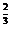 ,1.1
,1.1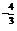 ;
;
(3)3.8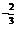 ,3.9
,3.9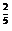 ,(-1.8)
,(-1.8) ; (4)31.4,51.5.
; (4)31.4,51.5.
当堂练习:
13.已知函数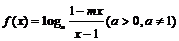 的图象关于原点对称. (1)求m的值;
的图象关于原点对称. (1)求m的值;
(2)判断f(x) 在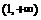 上的单调性,并根据定义证明.
上的单调性,并根据定义证明.
12.(1) 求函数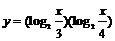 在区间
在区间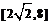 上的最值.
上的最值.
(2)已知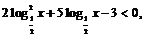 求函数
求函数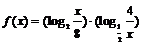 的值域.
的值域.
11.若集合{x,xy,lgxy}={0,|x|,y},则log8(x2+y2)的值为多少.
10.函数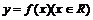 图象恒过定点
图象恒过定点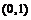 ,若
,若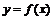 存在反函数
存在反函数 ,则
,则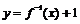 的图象必过定点 .
的图象必过定点 .
9.已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是 .
8.函数f(x)的定义域为[0,1],则函数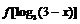 的定义域为
.
的定义域为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com