
5.某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3000+20x-0.1x2(0<x<240,x∈N),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是( )
A.100台 B.120台 C.150台 D.180台
4.在一次数学实验中, 运用图形计算器采集到如下一组数据.
|
x |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
|
y |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数) ( )
A.y=a+bX B.y=a+bx C.y=a+logbx D.y=a+b/x
3.某厂生产中所需一些配件可以外购,也可以自己生产,如外购,每个价格是1.10元;如果自己生产,则每月的固定成本将增加800元,并且生产每个配件的材料和劳力需0.60元,则决定此配件外购或自产的转折点是( )件(即生产多少件以上自产合算)
A.1000 B.1200 C.1400 D.1600
2.某商店卖A、B两种价格不同的商品,由于商品A连续两次提价20%,同时商品B连续两次降价20%,结果都以每件23.04元售出,若商店同时售出这两种商品各一件,则与价格不升、不降的情况相比较,商店盈利的情况是:( )
A.多赚5.92元 B.少赚5.92元 C.多赚28.92元 D.盈利相同
1.某物体一天中的温度T是时间t的函数: T(t)=t3-3t+60,时间单位是小时,温度单位是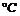 ,当t=0表示中午12:00,其后t值取为正,则上午8时的温度是( )
,当t=0表示中午12:00,其后t值取为正,则上午8时的温度是( )
A.8 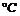 B.112
B.112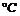 C.58
C.58 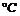 D.18
D.18
14.讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实根个数.
 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.6函数模型及其应用
重难点:将实际问题转化为函数模型,比较常数函数、一次函数、指数函数、对数函数模型的增长差异,结合实例体会直线上升、指数爆炸、对数增长等不同类型的函数增长的含义.
考纲要求:①了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义;
②了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
经典例题:1995年我国人口总数是12亿.如果人口的自然年增长率控制在1.25%,问哪一年我国人口总数将超过14亿.
当堂练习:
13. 已知二次函数 且满足
且满足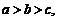
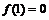 .
.
(1)证明:函数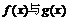 的图象交于不同的两点A,B;
的图象交于不同的两点A,B;
(2)若函数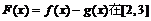 上的最小值为9,最大值为21,试求
上的最小值为9,最大值为21,试求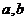 的值;
的值;
(3)求线段AB在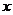 轴上的射影A1B1的长的取值范围.
轴上的射影A1B1的长的取值范围.
12.已知二次函数f(x)=a(a+1)x2-(2a+1)x+1,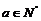 .
.
(1)求函数f(x)的图象与x轴相交所截得的弦长;
(2) 若a依次取1,2,3,4,---,n,时, 函数f(x)的图象与x轴相交所截得n条弦长分别为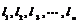 求
求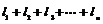 的值.
的值.
11.关于x的方程mx2+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.
10.已知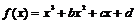 ,在下列说法中:
,在下列说法中:
(1)若f(m)f(n)<0,且m<n,则方程f(x)=0在区间(m,n)内有且只有一根;
(2) 若f(m)f(n)<0,且m<n,则方程f(x)=0在区间(m,n)内至少有一根;
(3) 若f(m)f(n)>0,且m<n,则方程f(x)=0在区间(m,n)内一定没有根;
(4) 若f(m)f(n)>0,且m<n,则方程f(x)=0在区间(m,n)内至多有一根;
其中正确的命题题号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com