
20. (1)∵f(x)与直线相切于(1,-11)
∴f(1)=-11,即1-3a+3b=1…………………………………①
∵f'(x)=3x2-6ax+3b,直线y =-12+1
=-12+1
∴f'(1)=3-6ax+3b=-12……………………………………②
①②联立方程组可得:a=1,b=-3
(2)由①可知:f(x)=x3-3x2-9 x
x
f'(x)=3x2-6x-9=3(x+1)(x-3)
令f'(x)>0,则x∈(-∞,-1)、(3,∞)为增函数。
令f'(x)<0,则x∈(-1,3)为减函数。
21(1)当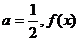 有最小值为
有最小值为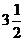 。
。
(2)当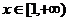 ,使函数
,使函数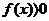 恒成立时,故
恒成立时,故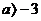
18.(本小题满分12分)
解:(1)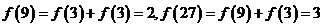
(2)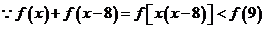
而函数f(x)是定义在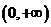 上为增函数
上为增函数

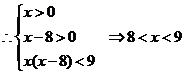
即原不等式的解集为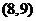
22.已知函数 ,
,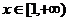
①当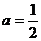 时,求函数
时,求函数 的最小值。
的最小值。
②若对任意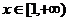 ,
, >
>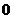 恒成立,试求实数
恒成立,试求实数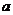 的取值范围。
的取值范围。


(Ⅱ)∵
∴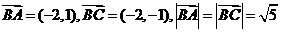 ,
,
∴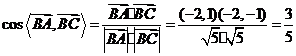
故 的值为
的值为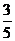 .
.
21.知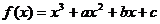 在
在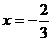 与
与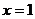 时都取得极值。
时都取得极值。
(1)求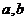 的值;
的值;
(2)若对 恒成立,求
恒成立,求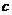 的取值范围。
的取值范围。
20.函数f(x)=x3-3ax2+3bx的图象与直线12x+y-1=0相切于点(1,-11)。
(1)求a, b的值;
(2)讨论函数f(x)的单调性。
19.已知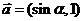 ,
,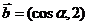 ,
,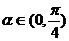
(1)若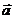 ∥
∥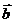 ,求
,求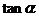 的值; (2)若
的值; (2)若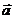 ·
·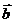
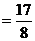 ,求
,求
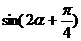 的值。
的值。
18.已知函数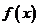 在定义域
在定义域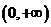 上为增函数,且满
上为增函数,且满 足
足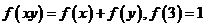
(1) 求
求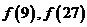 的值
(2)解不等式
的值
(2)解不等式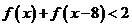

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com