
4.(2010·四川泸州)下列句子中没有语病的一项是
A. 面对西方文化的全面冲击,自觉传承华夏文明就成了每一个中国人义不容辞的责任。
B. 2010年,在我国南方抗旱救灾中,涌现出了一大批感人至深,令人敬仰的英雄事迹。
C. 一个卫生城市的标志不仅在于环境的洁净,更是在于广大市民卫生素养、文明意识。
D. 是否选择对社会对未来负责的低碳生活方式,是衡量现代人良好文明素质的重要标准。
[泸州答案]A
3.(2010四川乐山)病句修改。(4分)
下面两个句子都是出自中学语文教材,都有问题。请你选择一个句子作答。(两个句子都选了的,只评阅前一句)
①“深宵灯火是他的伴侣,因它大开光明之路,‘漂白了的四壁’。”
有老师认为应该改为:“深宵灯火是他的伴侣,因它大开光明之路,‘漂白了’‘四壁’。”你的看法呢?
答: [来源:Z*X*X*K]
②“他的眼神即使到美国治好后也还是不大好,走起路来有点深一脚浅一脚。”
这个句子应该做点修改,表达的意思才能清楚。请写出你修改后的句子。
答:
[乐山答案](4分)
①答:原文加了“的”字后,使“漂白了的四壁”变成了偏正短语,与“大开光明之路”动宾短语不一致,并且这个偏正短语不能作主语“它”的谓语。“漂白了四壁”是动宾短语,能作主语“它”的谓语,即“它大开……它漂白……”。
(注意答案是否能区分偏正短语与动宾短语,酌情给分。)
②答:这句话本来说的是他有眼疾,后来到美国治疗好了,但视力却没有恢复到正常人的程度,因此,走起路来深一脚浅一脚的。应该改为:他的眼神虽然到美国治疗过但还是不大好,走起路来有点深一脚浅一脚。
(酌情给分。改“眼神”为“眼力”的,得2分。)
4.上文划线句子有语病,请将修改后的正确语句写在下面横线上。(2分)
划线句:保护地球,维护人类发展与生存是人类共同的、也是唯一的选择。
应改为:
[达州答案](2分)应改为:良好的环境是人类生存与发展的基础。
22.(本小题满分12分)
已知双曲线C的中心在原点,焦点在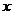 轴上,右准线为
轴上,右准线为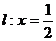 ,一条渐近线的方程是
,一条渐近线的方程是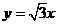 ,过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是PQ的中点。
,过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是PQ的中点。
(1)求双曲线C的方程;
(2)若A、B分别是双曲C的两条渐近线上的动点,且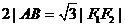 ,求线段AB的中点M的轨迹方程,并说明该轨迹是什么曲线;
,求线段AB的中点M的轨迹方程,并说明该轨迹是什么曲线;
(3)若在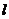 的左侧能作出直线
的左侧能作出直线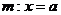 ,使点R在直线
,使点R在直线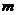 上的射影S满足
上的射影S满足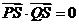 ,当点P在曲线C上运动时,求
,当点P在曲线C上运动时,求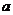 取值范围。
取值范围。
21.(本小题满分12分)
已知函数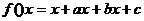 的图象经过原点,
的图象经过原点,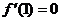 曲线
曲线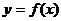 在原点处的切线到直线
在原点处的切线到直线 的角为135°。]
的角为135°。]
(1)求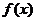 的解析式;
的解析式;
(2)若对于任意实数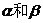 ,不等式
,不等式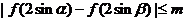 恒成立,求
恒成立,求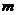 的最小值。
的最小值。
20.(本小题满分12分)
已知等差数列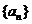 为递增数列,且
为递增数列,且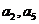 是方程
是方程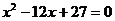 的两根,数列
的两根,数列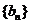 的前
的前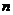 项和
项和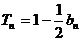 ;
;
(1)分别写出数列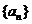 和
和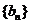 的通项公式;
的通项公式;
(2)记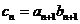 ,求证:数列
,求证:数列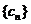 为递减数列。
为递减数列。
19.(本小题满分12分)
如图,直三棱柱A1B1C1-ABC中,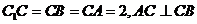 ,D、E分别为棱
,D、E分别为棱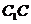 =B1C1的中点。
=B1C1的中点。
(1)求A1B与平面A1C1CA所成角的大小;
(2)求二面角B-A1D-A的大小;
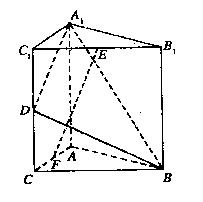 (3)在线段AC上是否存在一点F,使得
(3)在线段AC上是否存在一点F,使得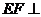 平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由。
平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由。
18.(本小题满分12分)
某工厂组织工人参加上岗测试,每位测试者最多有三次机会,一旦某次测试通过,便可上岗工作,不再参加以后的测试;否 则就一直测试到第三次为止。设每位工人每次测试通过的概率依次为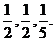
(1)若有3位工人参加这次测试,求至少有一人不能上岗的概率;
(2)若有4位工人参加这次测试,求至多有2人通过测试的概率。(结果均用分数表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com