
19.排列与组合试题(自我检测)
填空题:
20.甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为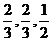 且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量ε分布列和数学期望;
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量ε分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
19. 已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率; (Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设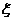 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求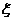 的分布列和数学期望.
的分布列和数学期望.
18.设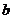 和
和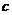 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量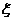 表示方程
表示方程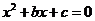 实根的个数(重根按一个计). (Ⅰ)求方程
实根的个数(重根按一个计). (Ⅰ)求方程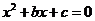 有实根的概率; (Ⅱ)求
有实根的概率; (Ⅱ)求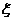 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程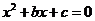 有实根的概率.
有实根的概率.
17.随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获利分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为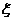 .
.
(1)求ξ的分布列; (2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%. 如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
16.设进入某商场的每一位顾客购买甲种商品的概率为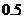 ,购买乙种商品的概率为
,购买乙种商品的概率为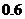 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记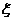 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求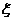 的分布列及期望。
的分布列及期望。
15. 甲、乙、丙3人投篮,投进的概率分别是, , .
(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;
(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
14.接种某疫苗后,出现发热反应的概率为0.80,现有5人接种了该疫苗,至少有3人出现发热反应的概率为 。(精确到0.01)
13.在某项测量中,测量结果x服从正态分布N(1,s2)(s)0),若x在(0,1)内取值的概率为0.4,则x在(0,2)内取值的概率为 。
12.在五个数字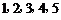 中,若随机取出三个数字,则剩下两个数字都是奇数的概率是 (结果用数值表示).
中,若随机取出三个数字,则剩下两个数字都是奇数的概率是 (结果用数值表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com