
4. 长方体的主视图与左视图如图3所示(单位:cm),则其俯视图的面积是( ).
(A) 12cm2. 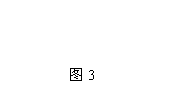
(B) 8cm2.
(C) 6cm2.
(D) 4cm2.
3. 如图2是某直观图三视图,那么对应的直观图是( ).
如图2是某直观图三视图,那么对应的直观图是( ).
2. 在水平的讲台上放置圆柱形水杯和长方体形粉笔盒(如图1),则它的主视图是( ).

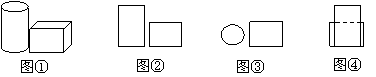
(A)图① (B)图② (C)图③ (D)图④
1. 下列图形中不是正方体平面展开图的是 ( ).

(五)、提高选择题与填空题的解题速度
解题的基本原则是“小题不能大做”.解题的基本策略是:巧做.解题的基本方法一
般有:直接求解法,图像法和特殊化法(特殊值法,特殊函数法,特殊角法,特殊数列法,图形特殊位置法,特殊点法,特殊方程法,特殊模型法)等.
考题类型举例:
(1)选择题与填空题
1.(直接法) 是虚数单位,若
是虚数单位,若 ,则
,则 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.
2.(直接法)下列说法错误的是
A. 满足线性回归方程
满足线性回归方程 ;
;
B.“ ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件;
C.在一个 列联表中,由计算得
列联表中,由计算得 ,则其两个变量间有关系的可能性是
,则其两个变量间有关系的可能性是 ;
;
D.命题 ,使得
,使得 的否定
的否定 是
是 ,均有
,均有 。
。
3.(直接法)某地区的一种特色水果上市时间仅能持续几个月,预测上市初期和后期会因供不应求使价格呈连续上涨的态势,而中期又将出现供大于求使价格连续下跌,为准确研究其价格走势,下面给出四个价格模拟函数中适合的是(其中为 常数,
常数, ,且
,且 )
)
A. B.
B.
C. D.
D.
4.(直接法)如果两个位数相同的自然数恰好只有某一数位上的数字不相同,则称这两个数为相邻数.例如:123与103、5555与5565分别是两个相邻数.若集合 中的元素均为两位数,且任意两个数都不是相邻数,则
中的元素均为两位数,且任意两个数都不是相邻数,则 中的元素最多有
中的元素最多有
A.8 个 B.9 个 C.11个 D.12个
5.(代入法)已知等差数列 ,等比数列
,等比数列 ,则该等差数列的公差为( )
,则该等差数列的公差为( )
A. 或
或 B.
B. 或
或 C.
C. D.
D.
6.(图解法)定义在 上的函数
上的函数 是减函数,且函数
是减函数,且函数 的图象关于
的图象关于 成中心对称,若
成中心对称,若 ,
, 满足不等式
满足不等式 .则当
.则当 时,
时, 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
7.(图解法)函数 图像上关于原点对称点共有
图像上关于原点对称点共有
A.0对 B.1对 C.2对 D.3对
8.(特值代验)设 ,那么( )
,那么( )
A. B.
B. C、
C、 D.
D.
9.(特值代验)设 表示不超过
表示不超过 的最大整数(如:
的最大整数(如: ,
, ),则定义在
),则定义在 的
的
函数 的值域为
的值域为
A. B.
B.
C. D.
D. .
.
10.(估值法) 在直角坐标平面上,已知A(-7,0)、B(3,0),点C在直线 上,若∠ACB >
上,若∠ACB > ,则点C的横坐标的取值范围是
,则点C的横坐标的取值范围是
A. B.
B. C.
C. D.
D.
11.(直接法)某单位为了了解用电量y度与气温 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
|
气温(0C) |
18 |
13 |
10 |
-1 |
|
用电量(度) |
24 |
34 |
38 |
64 |
用线性回归分析,预测当气温为 时,用电量的度数约为 __.(精确到1)
时,用电量的度数约为 __.(精确到1)
12.(直接法)我们可以用随机数法估计 的值,右边程序框图表示其基本步骤
的值,右边程序框图表示其基本步骤
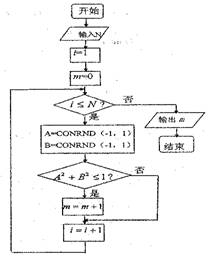 (假设函数
(假设函数 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生
内的任何一个实数).如果输入2000,输出的结果为1572,则由此
可估计 的近似值为
.(保留4位有效数字)
的近似值为
.(保留4位有效数字)
13.(直接法)在 中,角
中,角 所对的边分别为
所对的边分别为 ,
, 表示
表示
 的面积,若
的面积,若 ,
,
则 .
.
14.如果x+x2+x3+……+x9+x10
=a0+a1(1+x)+a2(1+x)2+……+a9(1+x)9+a10(1+x)10,则a9=___ ____.
15.(特例法)已知真命题:过抛物线 的顶点
的顶点 作两条互相垂直的直线,分别交抛物线于另外两点
作两条互相垂直的直线,分别交抛物线于另外两点 ,则直线
,则直线 过定点
过定点 .类比此命题,写出关于椭圆
.类比此命题,写出关于椭圆 的一个真命题:
.
的一个真命题:
.
(2)选考题
坐标系:①已知直线 过点
过点 ,倾斜角为
,倾斜角为 ,定点
,定点 .若直线
.若直线 上的不同两点
上的不同两点 满足
满足 ,求
,求 的值.
的值.
②极坐标系中,求圆 上的点到直线
上的点到直线 距离的取值范围.
距离的取值范围.
不等式:已知 ,又
,又 的最大值为
的最大值为 .
.
(I) 求 的值
的值
(II) 若关于 的不等式
的不等式 有解,求
有解,求 的取值范围.
的取值范围.
(3) 数列:关于某港口今后20年的发展规划,有如下两种方案:
方案甲:按现状进行运营.据测算,每年可收入760万元,但由于港口淤积日益严重,从明年开始需投资进行清淤,第一年投资50万元,以后逐年递增20万元.
方案乙:从明年起开始投资6000万元进行港口改造,以彻底根治港口淤积并提高吞吐能力.港口改造需用时4年,在此期间边改造边运营.据测算,开始改造后港口第一年的收入为320万元,在以后的3年中,每年收入都比上一年增长50%,而后各年的收入都稳定在第4年的水平上.
(I)从明年开始至少经过多少年,方案乙能收回投资(累计总收益为正数)?
(II)从明年开始至少经过多少年,方案乙的累计总收益超过方案甲?(注:收益=收入-投资)
(4) 三角函数:已知 为锐角,且
为锐角,且 .
.
(I)求 的值;
的值;
(II) 求函数 (
( )的最大值和最小值.
)的最大值和最小值.
(5) 立体几何
已知多面体 中,
中,
 平面
平面 ,
,
 平面
平面 ,
,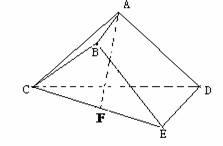
 ,
, .
. ,
, 为
为 的中点.
的中点.
(I)求证: 

 ;
;
(II)求平面 与平面
与平面 所成的锐二面角的大小;
所成的锐二面角的大小;
(III)求多面体 的体积.
的体积.
(6) 概率统计
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.


(I) 求全班人数及分数在 之间的频数;
之间的频数;
(II) 估计该班的平均分数;
(III) 若要从分数在 之间的试卷中任取4份分析学生失分情况,用
之间的试卷中任取4份分析学生失分情况,用 表示所抽取的试卷中分数在
表示所抽取的试卷中分数在 之间试卷的份数,求
之间试卷的份数,求 的分布列和数学期望.
的分布列和数学期望.
(7)解析几何
(本小题满分13分)如图,已知椭圆 过点
过点 ,且点
,且点 在
在 轴上的射影恰为椭圆的一个焦点.
轴上的射影恰为椭圆的一个焦点.
(I)求椭圆 的方程;
的方程;
(II)在下列两个小题中任选一题作答,若同时选做两题,则只批阅第(ii)小题,第(i)小题的解答,不管正确与否,一律视为无效,不予批阅.
(i)(解答本小题,满分6分)过 作两条倾斜角互补的直线与椭圆分别交于
作两条倾斜角互补的直线与椭圆分别交于 两点.试问:四边形
两点.试问:四边形 能否为平行四边形?若能,求出直线
能否为平行四边形?若能,求出直线 的方程;否则说明理由.
的方程;否则说明理由.
(ii)(解答本小题,满分9分)试问:是否存在斜率为定值的直线 交椭圆于不同的两点
交椭圆于不同的两点 ,使得直线
,使得直线 的倾斜角总是互补?若是,求出直线
的倾斜角总是互补?若是,求出直线 的方程;否则说明理由.
的方程;否则说明理由.
(8) 函数与导数
已知函数 .
.
(I)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(II)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(III)设函数 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(四)提高解选考题、数列(或三角)题、立体几何题、概率统计题的成功率
选考题、数列(或三角函数)、立体几何、概率统计题是“中等难度、高等得分”,抓好这些题的满分率是提高总分的有效途径.其中:
选考题关键是极坐标方程化直角坐标方程,参数方程化普通方程;利用柯西不等式证明不等式,求范围(最值)等,用图解法解决含绝对值不等式.
数列题关键是等差数列与等比数列的基本量的运算,关注数列应用题.
三角函数题关键是图像与性质、简单的恒等变换,正弦定理和余弦定理的应用.
立体几何题关键是正确建立空间直角坐标系,用坐标法解决垂直、平行的证明,空间的三种角及距离的计算.
概率统计题关键是重视概率思想与统计思想,重视统计量及统计中数据处理的方法.
(三)突破一个“老大难”
高考阅卷启示:许多中上水平考生常在“会而不对、对而不全”上拉开录取与落榜的距离;这是一个“老大难”问题.
(1)会而不对:做高考题目时不是束手无策,而是在正确的思路上,或考虑不周、或推理不严、或书写不准,最后答案是错的,这叫“会而不对”.
(2)对而不全:做题思路大体正确,最终结论也出来了,但丢三落四,或缺欠重大步骤,中间某一逻辑点过不去;或遗漏某一特殊情况、讨论不够完备;或潜在假设、或以偏概全,这叫“对而不全”.
为此必须综合治理,考试中会做的题目,要特别注意表达的准确、考虑的周密,书写的规范、语言的科学,做到“会而对、对而全、全而优”。
(二)掌握高考解题的思维规律
解高考题与平时作业不同之处在于他在特殊环境下和特定的条件下完成的,其中最显著的特点是严格受时间的限制,因此解高考题必须做到:
①迅速解决“从何处着手”;②迅速解决“向何方前进”; ③立足中下题目,力争高水平;
④立足一次成功,重复复查环节.复查应“以粗为主,粗细结合”,其主要目的在于看题目是否遗漏﹖题意是否弄错﹖要求是否符合﹖解题过程是否合理﹖步骤是否完整﹖结果是否科学﹖其复查方法主要有:复查核对、逆向运算、观测估算、特值检验、条件检验、逻辑检验等.
(一)三点建议
1、保持内紧外松的临战状态
2、使用适应高考的策略
3、运用应对选拔的考试技术
高考是选拔性考试,从技术上考虑,有两点建议,即制定科学的解题程序,树立“进入录取线”的全局意识.这就是说要尽量避免因“顺序答题、自然书写”所带来的常规性的失分,对此提出两点建议:
(1) 提前进入角色: 提前进入角色是拿到试卷前半小时,应让细胞开始简单数学活动,让大脑进入单一的数学情景,这不仅能转移临考前的焦虑,而且有利于把最佳竞技状态带进考场,这个过程跟体育比赛中“热身”一样,具体操作如下:清点用具是否齐全,把一些重要的数据,常用的公式,重要的定理过过电影,同学之间互问互答一些不大复杂的问题,但要注意提出的问题不能太难,否则回出现紧张情绪,最后看一眼难记易忘的结论.
(2)答题”一快一慢” .这就是说审题要慢,答题要快.审题要慢:是说题目本身包含无数个信息,问题是你将如何将这无数个信息通过加工、整理成你的有用的东西.这就是需要逐字逐句看清楚,力求从语法结构、逻辑关系、数学含义、解答形式、数据要求等各方法弄懂这一步不要怕慢.“成也审题,败也审题” .
(二)考前五天“巧”安排
1、 6月2日至4日---前三天模拟期
这两天建议考生完全对应高考7、8日两天的考试日程安排进行模拟训练.每天限定时间做一张模拟卷,让你的应试状态和生理兴奋点都能调节到最佳状态.
2、6月5日、6日---后两天休整期
考前最后的两天,不主张考生再进行集中、大量的复习.5日白天可以就前两天模拟卷上反映的问题再进行一次查漏补缺.晚上,开始整理好考试必要的物品,如果有缺漏的还能有时间及时补上.到了6日,希望还是以休息、放松心情为主.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com