
6.对a,b∈R,记max{a,b}= .函数f(x)=max{|x+1|,|x-2|}(x∈R)的最小
.函数f(x)=max{|x+1|,|x-2|}(x∈R)的最小
值是 ( )
A.0 B. C. D.3
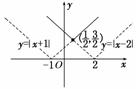
解析:函数f(x)=max{|x+1|,|x-2|}(x∈R)的图象如图所示,
由图象可得,其最小值为.
答案:C
5.若函数y=f(x)的值域是[,3],则函数F(x)=f(x)+的值域是
A.[,3] B.[2,] C.[,] D.[3,]
解析:令t=f(x),则≤t≤3,由函数g(t)=t+在区间[,1]上是减函数,在[1,3]上是增函数,则g()=,g(1)=2,g(3)=,故值域为[2,].
答案:B
4.若函数f(x)=(a2-2a-3)x2+(a-3)x+1的定义域和值域都为R,则a的取值范围是( )
A.a=-1或3 B.a=-1
C.a>3或a<-1 D.-1<a<3
解析:若a2-2a-3≠0,则函数为二次函数,不可能定义域和值域都为R,当a2-2a-3=0时,得a=-1或3,但当a=3时,函数为常数函数,也不可能定义域和值域都为R,故a=-1.
答案:B
3.若函数f(x)的定义域是[0,1],则f(x+a)·f(x-a)(0<a<)的定义域是 .
解析:∵f(x)的定义域为[0,1],
∴要使f(x+a)·f(x-a)有意义,
须
且0<a<,a<1-a,∴a≤x≤1-a.
答案:[a,1-a]
|
题组二 |
函数的值域问题 |
2.若函数y=的定义域为R,则实数m的取值范围是 ( )
A.(0,) B.(-∞,0)∪(0,+∞) C.(-∞,0]∪[,+∞) D.[0,)
解析:依题意,函数的定义域为R,
即mx2+4mx+3≠0恒成立.
①当m=0时,得3≠0,故m=0适合,可排除A、B.
②当m≠0时,16m2-12m<0,
得0<m<,综上可知0≤m<,排除C.
答案:D
1.(文)(2009·江西高考)函数y=的定义域为 ( )
A.[-4,1] B.[-4,0) C.(0,1] D.[-4,0)∪(0,1]
解析:求y=的定义域,
即 ⇒[-4,0)∪(0,1].
⇒[-4,0)∪(0,1].
答案:D
(理)(2009·江西高考)函数y=的定义域为 ( )
A.(-4,-1) B.(-4,1) C.(-1,1) D.(-1,1]
解析:定义域 ⇒-1<x<1.
⇒-1<x<1.
答案:C
12.下面是一个电子元件在处理数据时的流程图:
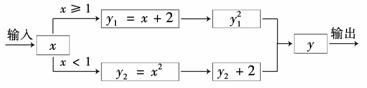
(1)试确定y与x的函数关系式;
(2)求f(-3)、f(1)的值;
(3)若f(x)=16,求x的值.
解:(1)y=
(2)f(-3)=(-3)2+2=11;f(1)=(1+2)2=9.
(3)若x≥1,则(x+2)2=16,
解得x=2或x=-6(舍);
若x<1,则x2+2=16,
解得x=(舍)或x=-.
即x=2或x=-.
11.如果f(a+b)=f(a)·f(b),且f(1)=2,则+++…+++= .
解析:f(2)=f(1)f(1)=22,=2,
f(3)=f(1)f(2)=23,f(4)=f(2)f(2)=24,
=2,…=2,
∴原式=2×1005=2010.
答案:2010
10.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s看作时间t的函数,其图象可能是 ( )
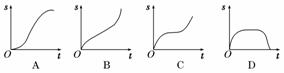
解析:画出曲线的切线,其切线的斜率的意义为速度.由图中切线斜率的变化规律可知选A.
答案:A
9.已知f(x)= 且f(a)=3,求a的值.
且f(a)=3,求a的值.
解:①当a≤-1时,f(a)=a+2,
由a+2=3,得a=1,与a≤-1相矛盾,应舍去.
②当-1<a<2时,f (a)=2 a,
由2a=3,得a=,满足-1<a<2.
③当a≥2时,f (a)= ,
,
由 =3,得a=±,又a≥2,∴a=.
=3,得a=±,又a≥2,∴a=.
综上可知,a的值为或.
|
题组四 |
函数及其表示的灵活应用 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com