4. 解．(1)根据动能定理：

　　　　　　　　 　　　mglsin60° - qU_BA = 0 - 0 ，

B、A两点的电势差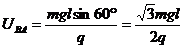　　

　　 (2)电场强度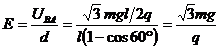　

　(3)小球到达B点时，悬线对小球的拉力T、重力沿半径方向的分力mgcos30°、电场力沿半径方向的分力qEcos60°的合力是向心力：

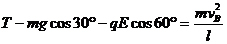
因为 　　　　　v_B = 0 ,

解得　　　 　　　T = 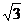mg。

3. 解：(1)两极间电压　　　　

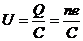
　　 　　 内部场强　　　　　　　　　　 　

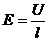
　　 　　 解出　　　　　　　　　　　　 　

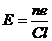
(2)设最多能有n’个电子到达B板，则第n’个电子在到达B板时速度恰减为0。

满足　　　　　　　　　　　　　 　

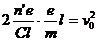
解出　　　　　　　　　　　　　

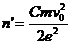
(3)第1个电子在两板间作匀速运动，运动时间为　

　　 最后1个电子在两板间作匀减速运动，到达B板时速度恰为0，运动时间为

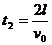
　　　 二者时间之差为　　　　　　　

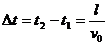
2.(1)200V/m；(2)－1V。

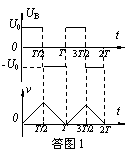
1.(1)当t＝0时，电子进入场区，根据运动和力的关系，可画出粒子运动速度随时间变化的关系图象(如答图1所示)。由图象可知，因图线与时间轴所围的面积总在速度轴的正值一侧，说明粒子的位移方向总沿同一方向，即一直朝B板运动。由图象还可看出，粒子的具体运动情况是：先加速、再减速，当速度减为零后继而又开始加速、再减速……，如此不断循环地变化而向B板运动。

(2)当t＝T/8时，电子进入场区，参照上述的方法分析，可以得出答案：电子时而向B板运动，时而向A板运动，最终到达B板。

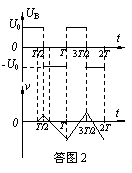
(3)当t＝3T/8时，电子进入场区，此时仍按上述思路画出粒子运动速度随时间变化的图象(如答图2所示)。由图象可知，粒子向正方向(B板)和负方向(A板)都将发生位移，得负方向的位移大于正方向的位移，所以粒子将在电压变化的第一个周期内被推出场区，而无法到达B板。

(4)对于t＝T/2时电子进入场区的情况，依照上述思路分析得出的答案是：粒子在刚一进入场区时，即被推出，故也不能到达B板。

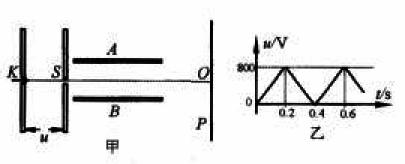
10.如图甲所示，真空中的电极K连续不断地发出电子(电子的初速度可忽略不计)，经电压为u的电场加速，加速电压u随时间t变化的图象如图乙所示。每个电子通过加速电场的过程时间极短，可认为加速电压不变。电子被加速后由小孔S穿出，沿两个彼此靠近且正对的水平金属板A、B间中轴线从左边缘射入A、B两板间的偏转电场，A、B两板长均为L=0.20m，两板之间距离d=0.050m，A板的电势比B板的电势高。A、B板右侧边缘到竖直放置的荧光屏P(面积足够大)之间的距离b=0.10m。荧光屏的中心点O与A、B板的中心轴线在同一水平直线上。不计电子之间的相互作用力及其所受的重力，求：

(1)要使电子都打不到荧光屏上，则A、B两板间所加电压U应满足什么条件；

(2)当A、B板间所加电压U'=50V时，电子打在荧光屏上距离中心点O多远的范围内。

9. 如图所示，水平绝缘光滑轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接，圆弧的半径R=0.40m。在轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×10⁴ N/C。现有一质量m=0.10kg的带电体(可视为质点)放在水平轨道上与B端距离s=1.0m的位置，由于受到电场力的作用带电体由静止开始运动，当运动到圆弧形轨道的C端时，速度恰好为零。已知带电体所带电荷q=8.0×10^-5C，取g=10m/s²，求：

(1)带电体在水平轨道上运动的加速度大小及运动到B端时的速度大小；

(2)带电体运动到圆弧形轨道的B端时对圆弧轨道的压力大小；

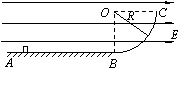(3)带电体沿圆弧形轨道运动过程中，电场力和摩擦力对带电体所做的功各是多少。

8.如图13，一长为L的绝缘细线下端系质量为m的金属小球，并带有 -q的电荷量，在细线的悬点o处放一带电荷量为+q的点电荷。要使金属球能在竖直平面内做完整的圆周运动，求：

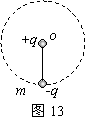　　 (1)金属球在最高点的最小速度值是多大？

(2)如果金属球刚好通过最高点，则它通过最低点时的速度多大？

7. 如图12所示，有彼此平行的A、B、C三块金属板于电源相接，B、A间相距为d₁，电压为U₁；B、C间相距为d₂，电压为U₂，且U₁<U₂。一个电子(电荷量e质量m)从紧靠A极板处由静止释放，经电压U₁加速后沿直线从B极板中央小孔进入BC极板间。若不计重力，求:

　　 (1)电子在BC板间前进的距离L；

(2)电子往复运动的周期T。

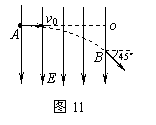
6. 如图11所示，a 粒子从A点以v₀的速度沿垂直电场线方向的直线AO方向射入电场，由B点飞出匀强电场时速度方向与AO方向成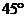。已知a 粒子质量为m，电荷量为2e。求OB两点间电势差。

5. 某平行板电容器，当其所带电荷量增加ΔQ=2.0×10^－9C时，两极板间电压增加了ΔU=5V。求：

(1)该电容器的电容是多少？

(2)当电容器两极板间电压为50V时，其所带电荷量为多少？