
3、思考讨论:
⑴根据段意,完成下面的填空题,概括各段的内容:
第一段:故山殊可过,而今 。
第二段:故山冬夜 ,静默独坐,多思 。
第三段:故山春景 ,只想 。
提示:
第一段:故山殊可过,而今我独过。
第二段:故山冬夜,清丽淡远,宁静和谐,静默独坐,多思 与你同游,携手赋诗。
第三段:故山春景 斑斓夺目,生机勃勃 ,只想 邀你同游 。
(2)文中有一个词浓缩了本文的主要内容,是本文的“文眼”,请你找出这个词,并说说它包含了哪些内容?
提示:“深趣”是文眼。它包括王维笔下的终南美景,主要是冬夜清丽淡远、宁静和谐的氛围和春天色彩斑斓、生机勃勃的景象,还有朋友相邀的一片诚心。
第二课时
教学要点:
重点分析文中的写景;品读课文,体会“深趣”,理解创作风格。
教学过程:
2、学生齐读课文,教师正音。
1、学生自由诵读,借助注释和工具书感知课文。
王维于天宝三载(744)在蓝田购买了辋川别业。每到休假之时,他便来到那里,过着半官半隐的生活。这时朝政由奸相李林甫把持,有才能和敢于直言谏诤的人,纷纷受到压制、打击。在这种情况下,王维早年经国济民的心志开始冷淡下来,他要在山水之间寻求宁静、安逸的生活环境,以洁身自好,躲避政治风险。
王维的辋川别业地处陕西蓝田南八里的峣山之口,辋谷水出峣山口北流入灞水。辋川别业傍山临水,风景非常优美。裴迪曾是辋川别业的常客,是王维寄情山水的同道。他们经常一起“浮舟往来,弹琴赋诗”,品尝山林隐逸生活的乐趣。这一年的腊月末,裴迪在自己家中温习经书,准备去应科举考试。王维居住在辋川别业颇有孤独之感,便写了这一封信给裴迪,约请他明年春天来这里与他同游。
王维(701—761),唐代诗人、画家。字摩诘。祖籍太原祁(今山西祁县),其父迁家蒲州(今山西永济),遂为蒲人。他官终尚书右丞,世称“王右丞”。
王维青少年时即富于文学才华。开元九年(721)中进士第,为大乐丞。因故谪济州司仓参军。后归至长安。开元二十二年张九龄为中书令,王维被擢为右拾遗。二十四年张九龄罢相,次年贬荆州长史,李林甫任中书令,这是玄宗时期政治由较为清明而日趋黑暗的转折点。开元二十五年,曾奉使赴河西节度副大使崔希逸幕,后又以殿中侍御史知南选,天宝中,王维的官职逐渐升迁。他原信奉佛教,此时随着思想日趋消极,其佛教信仰也日益发展。他青年时曾居住山林,中年以后一度家于终南山,后又得宋之问蓝田辋川别业,遂与好友裴迪优游其中,赋诗相酬为乐。天宝十五载(756)安史乱军陷长安,玄宗入蜀,王维为叛军所获。服药佯为瘖疾,仍被送洛阳,署以伪官。两京收复后,受伪职者分等定罪,他因所作怀念唐室的《凝碧池》诗为肃宗嘉许,且其弟王缙官位已高,请削官为兄赎罪,故仅降职为太子中允,后复累迁至给事中,终尚书右丞,世称王右丞。
王维诗现存不满400首。其中最能代表其创作特色的是描绘山水田园等自然风景及歌咏隐居生活的诗篇。过去时代不少人推崇王维此类诗歌,一方面固然由于它们具有颇高的艺术技巧,一方面也由于对其中体现的闲情逸致和消极思想产生共鸣。明代胡应麟称王维五绝“却入禅宗”,又说《鸟鸣涧》《辛夷坞》二诗,“读之身世两忘,万念皆寂”(《诗薮》),便是一个明证。
王维其他题材的作品,如送别、纪行之类的诗中,也经常出现写景佳句,如“远树带行客,孤城当落晖”(《送綦毋潜落第还乡》)、“山中一半雨,树杪百重泉”(《送梓州李使君》)、“日落江湖白,潮来天地青”(《送邢桂州》)、“大漠孤烟直,长河落日圆”(《使至塞上》)等,都是传诵不衰的名句。
苏轼曾说:“味摩诘之诗,诗中有画;观摩诘之画,画中有诗。”(《东坡题跋·书摩诘蓝田烟雨图》)王维不但有卓越的文学才能,而且是出色的画家,还擅长音乐。他的诗取景状物,极有画意,色彩映衬鲜明而优美,写景动静结合,尤善于细致地表现自然界的光色和音响变化
王维描绘自然风景的高度成就,使他在盛唐诗坛独树一帜,成为山水田园诗派的代表人物。他继承和发展了谢灵运开创的写作山水诗的传统,对陶渊明田园诗的清新自然也有所吸取,使山水田园诗的成就达到了一个高峰,因而在中国诗歌史上占有重要的位置。
昔人曾誉王维为“诗佛”,并与“诗圣”杜甫、“诗仙”李白并提。以思想内容而言,王维诗远不能与李、杜相提并论;而在艺术方面,王维确有其独特的成就与贡献。
[山中]点明地点。
[秀才]是唐代对中进士者的一种通称。
[裴迪]王维友人,曾任蜀州刺史,曾是辋川别业的常客,也是王维寄情山水的同道。
[书]点明了体裁。
王维是唐代著名的山水诗人,我们接触过其许多山水诗,给我们留下了深刻的印象,如《山居秋暝》《过香积寺》《鸟鸣涧》《鹿柴》,里面有许多脍炙人口的名句,“明月松间照,清泉石上流”“泉声咽危石,日色冷青松”“月出惊山鸟,时鸣春涧中”“空山不见人,但闻人语响”,写出了诗人追求人生宁静,闲适的境界。今天,我们学习他的一篇散文《山中与裴秀才迪书》,是否也有同样的人生境界?
20. (本小题满分14分)
在平面直角坐标系中, 为坐标原点,已知两点
为坐标原点,已知两点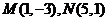 ,若动点
,若动点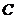 满足
满足
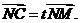 且点
且点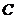 的轨迹与抛物线
的轨迹与抛物线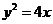 交于
交于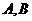 两点.
两点.
(1)求证: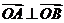 ;
;
(2)在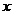 轴上是否存在一点
轴上是否存在一点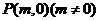 ,使得过点
,使得过点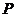 的直线
的直线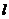 交抛物线
交抛物线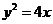 于
于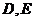 两点,并以线段
两点,并以线段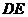 为直径的圆都过原点。若存在,请求出
为直径的圆都过原点。若存在,请求出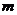 的值及圆心
的值及圆心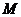 的轨迹方程;若不存在,请说明理由.
的轨迹方程;若不存在,请说明理由.
19.(本小题满分14分)已知函数 图象上一点
图象上一点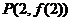 处的切线方程为
处的切线方程为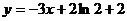 .
.
(1)求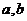 的值;
的值;
(2)若方程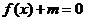 在
在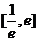 内有两个不等实根,求
内有两个不等实根,求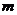 的取值范围(其中
的取值范围(其中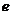 为自然对数的底数);
为自然对数的底数);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com