
55.[2010·安微八校第二次联考]已知圆C经过点A(2,-1),圆心在直线2x+y=0上,且与直线x+y=1相切,则圆C的标准方程是 .
[答案]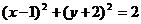
[解析]因为圆心C在直线2x+y=0上,可设圆心为C(a,-2a).则点C到直线x+y=1的距离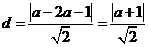 . 据题意,
. 据题意, ,则
,则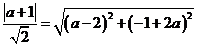 ,解得
,解得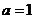 .所以圆心为C(1,-2),半径
.所以圆心为C(1,-2),半径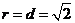 ,故所求圆的方程是
,故所求圆的方程是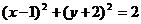 .
.
54.[2010·浙江省杭州市第二次质检]已知A、B是圆O:x2+y2=16上的两点,且|AB|=6,若以AB为直径的圆M恰好经过点C(1,-1),则圆心M的轨迹方程是 。
[答案](x-1)2+(y+1)2=9
[解析]因为点C(1,-1)在以AB为直径的圆M上,所以CM=AB=3,从而点M在以C为圆心,以3为半径的圆上。故点M的轨迹方程为(x-1)2+(y+1)2=9。
53.[2010·昌平区第二学期第二次统一练习]以点(-3,4)为圆心且与直线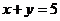 相切的圆的标准方程是 ______.
相切的圆的标准方程是 ______.
[答案](x+3)2+(y-4)2=8
[解析]由圆心到直线的距离r==2,所以圆的方程为(x+3)2+(y-4)2=8。
52.[2010·上海市普陀区4月质调]在复平面上,已知直线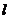 上的点所对应的复数
上的点所对应的复数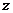 满足
满足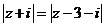 ,则直线
,则直线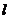 的倾斜角为 .(结果反三角函数值表示)
的倾斜角为 .(结果反三角函数值表示)
[答案]π-arctan.
[解析]由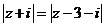 知,点Z位于线段AB(其中A(0,-1)与B(3,1))的垂直平分线上,kAB=,所以kl=-,从而倾角为π-arctan.
知,点Z位于线段AB(其中A(0,-1)与B(3,1))的垂直平分线上,kAB=,所以kl=-,从而倾角为π-arctan.
51.[2010·北京东城一模]经过点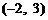 且与直线
且与直线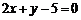 垂直的直线方程为
.
垂直的直线方程为
.
[答案]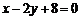
[解析]直线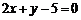 的斜率为
的斜率为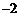 ,故所求直线的斜率为
,故所求直线的斜率为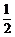 ,从而所求直线方程为
,从而所求直线方程为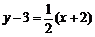 .
.
50.[2010·丰台一模]已知点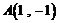 ,点
,点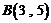 ,点
,点 是直线
是直线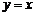 上动点,当
上动点,当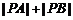 的值最小时,点
的值最小时,点 的坐标是
.
的坐标是
.
[答案]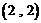
[解析]
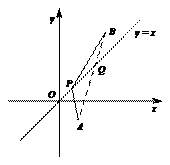
连结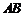 与直线
与直线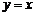 交于点
交于点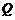 ,则当
,则当 点移动到
点移动到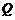 点位置时,
点位置时,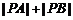 的值最小.
的值最小.
直线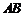 的方程为
的方程为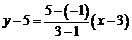 ,即
,即 .解方程组
.解方程组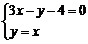 ,得
,得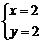 .于是当
.于是当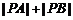 的值最小时,点
的值最小时,点 的坐标为
的坐标为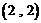 .
.
49.[2010·上海市黄浦区、嘉定区年一模]已知直线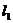 :
: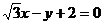 ,
,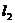 :
: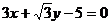 ,则直线
,则直线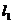 与
与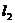 的夹角是 .
的夹角是 .
[答案]
[解析]因为直线l1的斜率为,故倾斜角为60°,直线l2的斜率为-,倾斜角为120°,故两直线的夹角为60°.
48.[2010·宁波市摸底考试]△AOB三个顶点分别为O(0,0),A(-3,4),B(0,10),则过点O将∠AOB的平分的直线方程为 。
[答案]3x+y=0
[解析]易知因为|OA|=5,|OB|=10,由三角形内角平分线性质知:所求直线与AB的交于点C,且分有向线段AB比为λ==,设C(x,y),则,故所求直线为y=-3x,即3x+y=0。
47.[2010·广东汕头考前模拟]在直线y=kx+b中,当x∈[-3,4]时,y∈[-8,13],则此直线方程为 .
[答案]y=3x+1或y=-3x+4
[解析]当k>0时,y=kx+b在[-3,4]上递增,所以直线y=kx+b过点(-3, -8),(4,13),于是,解之得,故直线方程为y=3x+1;
当k<0时,y=kx+b在[-3,4]上递减,所以直线y=kx+b过点(-3,13),(4,-8),于是,解之得,故直线方程为y=-3x+4。
46.[2010·东城区一模]经过点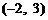 且与直线
且与直线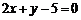 垂直的直线方程为 .
垂直的直线方程为 .
[答案]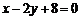
[解析]直线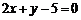 的斜率为
的斜率为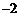 ,故所求直线的斜率为
,故所求直线的斜率为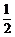 ,从而所求直线方程为
,从而所求直线方程为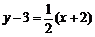 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com