
21. (12分)如图,线段AB经过x轴的正半轴上一点M(m, 0),两端点到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.
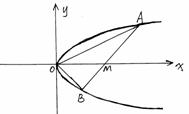 ⑴求抛物线方程
⑵若tan<AOB=-1,求m的最大值.
⑴求抛物线方程
⑵若tan<AOB=-1,求m的最大值.
20. (12分)在实数集R上定义运算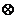 :x
:x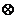 y=(x+a)(1-y),设f(x)=x2 g(x)=x
若F(x)=f(x)
y=(x+a)(1-y),设f(x)=x2 g(x)=x
若F(x)=f(x)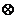 g(x)
⑴求F(x)的解析式
⑵若F(x)在R上是减函数,求a的取值范围
⑶若a=
g(x)
⑴求F(x)的解析式
⑵若F(x)在R上是减函数,求a的取值范围
⑶若a=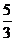 , 则在F(x)的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程。若不存在,说明理由.
, 则在F(x)的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程。若不存在,说明理由.
19. 
|



|
|
|


 (12分)如图所示,四棱锥P-ABCD中,底面ABCD是平行四边形,
∠DAB=60°,AB=2AD=2a,ΔPDC为正三角形, BC⊥PD
⑴证明:平面PBD⊥平面ABCD
⑵求二面角C-PD-B的正切值
⑶求点B到平面PAD的距离
(12分)如图所示,四棱锥P-ABCD中,底面ABCD是平行四边形,
∠DAB=60°,AB=2AD=2a,ΔPDC为正三角形, BC⊥PD
⑴证明:平面PBD⊥平面ABCD
⑵求二面角C-PD-B的正切值
⑶求点B到平面PAD的距离
18. (12分)甲、乙两人各进行3次射击,甲每次击中目标的概率为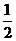 ,乙每次击中目标的概率为
,乙每次击中目标的概率为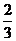 .
(1)求乙至多击中目标2次的概率
(2)求甲恰好比乙多击中目标2次的概率
(3)(理)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ.
.
(1)求乙至多击中目标2次的概率
(2)求甲恰好比乙多击中目标2次的概率
(3)(理)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ.
17. (本小题满分12分)已知向量m=(cos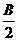 ,
, 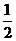 )与向量n=(
)与向量n=(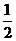 ,
cos
,
cos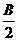 )共线,其中A、B、C是ΔABC的内角.
(l)求角B的大小;
(2)若cosC=
)共线,其中A、B、C是ΔABC的内角.
(l)求角B的大小;
(2)若cosC=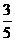 , 求cosA的值.
, 求cosA的值.
16. 已知球O的表面积为 4π,A,B , C 三点都在球面上,且任意两点间的球面距离为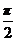 ,则OA与平面ABC所成角的正切值是
.
,则OA与平面ABC所成角的正切值是
.
15. (理)已知点P(x、y)满足不等式组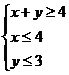 ,则|x+y+1|的取值范围是 .
(文)已知点P(x、y)满足不等式组
,则|x+y+1|的取值范围是 .
(文)已知点P(x、y)满足不等式组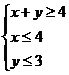 ,则
,则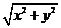 的取值范围是
.
的取值范围是
.
14. (x+2)(x-1)5展开式中x2的系数是 .(用数字作答)
13. 一个电视台在因特网上就观众对其某一节目的喜爱程度进行调查,调查的总人数为 1500人,其中持各种态度的人数如下表:
 电视台为了解观众的具体想法和意见,打算从中抽选出 150 人进行更为详细的调查,为此要进行分层抽样,那么在“喜爱”这类态度的观众中抽取的人数为
.
电视台为了解观众的具体想法和意见,打算从中抽选出 150 人进行更为详细的调查,为此要进行分层抽样,那么在“喜爱”这类态度的观众中抽取的人数为
.
12. 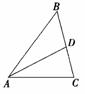 已知向量p、q的夹角为
已知向量p、q的夹角为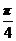 , 且|p|
=2
, 且|p|
=2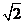 ,
|q|=3 ,若
,
|q|=3 ,若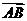 =5p+2q,
=5p+2q, 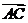 =p-3q,且D为线段BC的中点,则
=p-3q,且D为线段BC的中点,则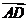 的长度为
A.
的长度为
A.
 B.
B. 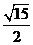 C. 7 D.
8
C. 7 D.
8
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com