
4. Pierre and I did have a good time at the ball.
3. I would rather not tell you.
2. It is dangerous or bad for your health.
1. There is no doubt that ...
下课后,万校长邀约我们到他的办公室座谈.当然,受邀的还有古老师本人和参与听课的教师.他们一致将目光射向我们,显然是希望我们首先发言.
我说:“从学生的反应来看,这节课的效果的确不错. 只是古老师这种‘三不’的教学方法,我们还是第一次见到.还需要很好的学习领会.”
G君说:“我们知道万校长也是教数学的行家里手,还是请万校长给我们作一个示范性的评讲吧.”
看来万校长真希望他们这位“三不教师”能够得到更大范围的理解,所以他毫无保留地连说了5个好字.他说:
“其一,虽然课堂上解决的题目不多,但是牵涉到的内容不少.讲课的基本原则是一定让学生听懂,会做.兵法有云:伤其十指不如断其一指.与其多讲许多题,使学生对每道题都一知半解,倒不如少讲,精练,解决一题是一题.所以仅从这一点来看,本课的教学效果良好.
其二,古老师上课的具体内容,是根据学生现场的要求和反应而定.做到有的放矢,解决最大多数学生的疑难.因为不可预料的情况出现,无法完成进度时,就见好就收.这里实行的是灵活机动的战略战术.
第三,古老师的教学方式是启发式.每道需要解决的题都有严密的教学设计.几个问题由浅入深,环环相扣,体现了循序渐进的教学原则.全堂课是在教师的主导作用下,几乎每个学生的积极性都调动起来了.凡是学生自己能够解决的,教师决不越俎代庖.这又是最难掌握的课堂艺术.
第四,古老师不用教辅,但使用了最简洁明了的对应试卷.课堂教学不求全,只求特,而且对即将到来的9月考针对性很强,这又符合以最小的代价争取最大效果的数学原则. 是十分大胆的教学革新.
最后,一堂课到底好不好,归根结底该学生说了算.这堂课学生的反应良好,他们学得积极,轻松,且负担不重,这对继续学好数学十分有利.
社会上传说古老师是‘三不教师’,这不完全符合实际.其一,他不用任何教辅,但是用了精辟得多的高考试卷和各种有价值的模拟试卷;其二,他的确没有完全按教学计划行事,那是因为计划是死的,课堂艺术是活的,能够根据课堂实践随时调整自己的教学进度和计划,这才是最难掌握的课堂艺术;其三,说古老师不布置任何作业是不符合事实的.只是他布置的作业相对要少一些,而且不一定是非得是必交的书面作业.就拿本节课来说,上课的前一天他就将试卷发给学生去思考,所以今天学生就能够明确提出希望他讲哪些题.本节课因故没有讲完,他也布置了思考性的作业.”
“万校长的精辟分析让我们大开眼界!”我说:“古老师何止是‘三不’,应该称为‘五不教师’,即不用任何教辅,不死板执行教学计划,不布置大量无效的作业,学生不完全搞懂时绝不抢进度,学生能够自己解决问题的,教师决不不越俎代庖.”
万校长显然十分高兴,说:“古老师还有一堂更为精彩的课,欢迎两位继续光临.”
事后我问万校长:“既然校长对古老师这样肯定,却为什么不肯推广他的经验?”
万校长只说了一句:“时机不成熟.”
欲知后事如何,请看下回:妙趣横生.
2.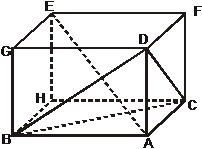 能够用a,b,c去表示这个四面体外接球的直径吗?
能够用a,b,c去表示这个四面体外接球的直径吗?
(有人提出:如图3-2,将此四面体补成长方体
ABHC-DGEF. 则原四面体与此长方体同一个外接球.其体对角线
是此球的直径,即有AE=2R.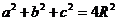 )
)
以下,古老师感到要下课了,立即收口:“今天只能讲到
|
听到满意的答案.”
果然,古老师再没有布置任何其他的作业,就这样下课了.不过我们感到,学生们的反应是出奇的好.
1. 如图3-1,设AB=a,AC=b,AD=c,那么
|
(几乎每个人都能够写出:  )
)
5.请大家具体设计一条直线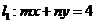 使得它与圆
使得它与圆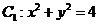 是相离的.
是相离的.
(在众多的数据设计中,古老师看中了一位同学的数据是:取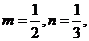 则直线
则直线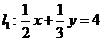 满足
满足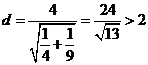 ,.故直线
,.故直线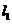 与圆
与圆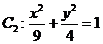 相离,即无公共点.这时点
相离,即无公共点.这时点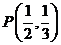 在椭圆
在椭圆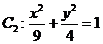 的内部.)
的内部.)
结果是这样直观易懂,乃至提出问题4的同学自动回答了自己提出的问题:“我明白了:作为方程的参数,直线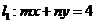 与圆相离,即直线到圆心的距离大于2;而作为点的坐标,点P(m,n)到原点的距离小于2,所以它在椭圆内部.”
与圆相离,即直线到圆心的距离大于2;而作为点的坐标,点P(m,n)到原点的距离小于2,所以它在椭圆内部.”
古老师终于可以让大家继续讨论第9题了.那道题是:
设A,B,C,D是半径为R的球面上四点,且AB,AC,AD两两垂直,则△ABC,△ABD,△ACD面积之和
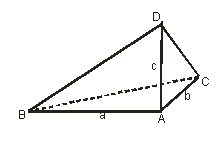
 的最大值为
的最大值为

可是,这道题古老师只来得及提出两个问题
4. 圆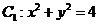 的半径是2,而直线
的半径是2,而直线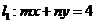 与圆相离;椭圆
与圆相离;椭圆 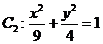 的短半轴也是2,点P(m,n)却在椭圆内部,怎么解释这两个矛盾的结论?
的短半轴也是2,点P(m,n)却在椭圆内部,怎么解释这两个矛盾的结论?
(显然,这个问题的提出超出了古老师的意料,一时难于讲清个中道理.但是他灵机一动,提出了:)
3.满足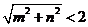 的点P(m,n)在椭圆的什么位置?
的点P(m,n)在椭圆的什么位置?
(多数人认识到:如图3,由于椭圆的短半轴为2,而点P(m,n)满足 ,即点P必在椭圆内部,这样过点P的直线必与椭圆有两个交点.同样地,古老师让一位解得较好的同学在黑板上写出了如下的
,即点P必在椭圆内部,这样过点P的直线必与椭圆有两个交点.同样地,古老师让一位解得较好的同学在黑板上写出了如下的
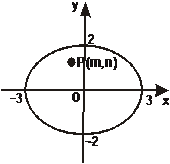 [解析]圆
[解析]圆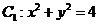 的圆心为原点O(0,0),半径r=2.
的圆心为原点O(0,0),半径r=2.
当直线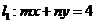 和圆
和圆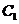 无公共点时, 圆心到直线
无公共点时, 圆心到直线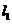 的距离d>2.即
的距离d>2.即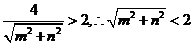 .即点P必在椭圆
.即点P必在椭圆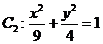 内部.
内部.
|
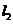 与椭圆必有两个公共点.选B.
与椭圆必有两个公共点.选B.
古老师准备满意地收场,继续讨论第9题时,却有人意外地提出问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com