
3. 
|
2. 有一种衰变叫EC衰变,EC衰变发生于核内中子数相对过少的放射性原子核,核内的一个质子(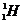 )可以俘获一个核外电子(
)可以俘获一个核外电子(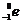 )并放射出一个中微子而转变为一个中子(
)并放射出一个中微子而转变为一个中子(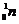 ).经过一次EC衰变后原子核的
A. 质量数不变,原子序数减少1
B. 质量数增加1,原子序数不变
C. 质量数不变,原子序数不变
D. 质量数减少1,原子序数减少1
).经过一次EC衰变后原子核的
A. 质量数不变,原子序数减少1
B. 质量数增加1,原子序数不变
C. 质量数不变,原子序数不变
D. 质量数减少1,原子序数减少1
1. 下列说法正确的是 A.布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映 B.没有摩擦的理想热机可以把吸收的能量全部转化为机械能 C.知道某物质的摩尔质量和密度可求出阿伏加德罗常数 D.内能不同的物体,它们分子热运动的平均动能可能相同
22. (14分)数列{an}中,a1=1, n≥2时,其前n项的和Sn满足:Sn2=an(Sn-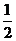 )
⑴求Sn的表达式;
⑵(文)设bn=
)
⑴求Sn的表达式;
⑵(文)设bn=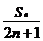 ,求数列{bn}前n项和Tn
,求数列{bn}前n项和Tn
 (理)设bn=
(理)设bn=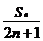 ,数列{bn}前n项和Tn,求:
,数列{bn}前n项和Tn,求: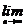 Tn.
Tn.
21. (12分)如图,线段AB经过x轴的正半轴上一点M(m, 0),两端点到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.
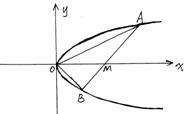 ⑴求抛物线方程
⑵若tan<AOB=-1,求m的最大值.
⑴求抛物线方程
⑵若tan<AOB=-1,求m的最大值.
20. (12分)在实数集R上定义运算 :x
:x y=(x+a)(1-y),设f(x)=x2 g(x)=x
若F(x)=f(x)
y=(x+a)(1-y),设f(x)=x2 g(x)=x
若F(x)=f(x) g(x)
⑴求F(x)的解析式
⑵若F(x)在R上是减函数,求a的取值范围
⑶若a=
g(x)
⑴求F(x)的解析式
⑵若F(x)在R上是减函数,求a的取值范围
⑶若a=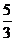 , 则在F(x)的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程。若不存在,说明理由.
, 则在F(x)的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程。若不存在,说明理由.
19. 
|



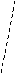
|
|
|


 (12分)如图所示,四棱锥P-ABCD中,底面ABCD是平行四边形,
∠DAB=60°,AB=2AD=2a,ΔPDC为正三角形, BC⊥PD
⑴证明:平面PBD⊥平面ABCD
⑵求二面角C-PD-B的正切值
⑶求点B到平面PAD的距离
(12分)如图所示,四棱锥P-ABCD中,底面ABCD是平行四边形,
∠DAB=60°,AB=2AD=2a,ΔPDC为正三角形, BC⊥PD
⑴证明:平面PBD⊥平面ABCD
⑵求二面角C-PD-B的正切值
⑶求点B到平面PAD的距离
18. (12分)甲、乙两人各进行3次射击,甲每次击中目标的概率为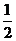 ,乙每次击中目标的概率为
,乙每次击中目标的概率为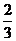 .
(1)求乙至多击中目标2次的概率
(2)求甲恰好比乙多击中目标2次的概率
(3)(理)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ.
.
(1)求乙至多击中目标2次的概率
(2)求甲恰好比乙多击中目标2次的概率
(3)(理)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ.
17. (本小题满分12分)已知向量m=(cos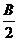 ,
, 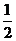 )与向量n=(
)与向量n=(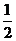 ,
cos
,
cos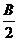 )共线,其中A、B、C是ΔABC的内角.
(l)求角B的大小;
(2)若cosC=
)共线,其中A、B、C是ΔABC的内角.
(l)求角B的大小;
(2)若cosC=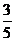 , 求cosA的值.
, 求cosA的值.
16. 已知球O的表面积为 4π,A,B , C 三点都在球面上,且任意两点间的球面距离为 ,则OA与平面ABC所成角的正切值是
.
,则OA与平面ABC所成角的正切值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com