1.已知cos(α－π)＝－，且α是第四象限角，则sin(－2π+α)＝样　　　　　　 (　)

A．－　 　　　B.　　　　　 C．± 　　　D.

解析：由cos(α－π)＝－得，cosα＝，而α为第四象限角，

∴sin(－2π+α)＝sinα＝－＝－.

答案：A

12．设0≤θ＜2π，如果sinθ＜0且cos2θ＜0，则θ的取值范围是　　　　　　 (　)

A．π＜θ＜　 　　　　B.＜θ＜2π

C.＜θ＜ 　　　　　D.＜θ＜

解析：∵0≤θ＜2π，且sinθ＜0，∴π＜θ＜2π，

又由cos2θ＜0得2kπ+＜2θ＜2kπ+，

即kπ+＜θ＜kπ+(k∈Z)，

∵π＜θ＜2π，∴k＝1，即θ的取值范围是＜θ＜.

答案：D

11．若θ为第一象限角，则能确定为正值的是　　　　　　　　　　　　　　　 (　)

A．sin 　　B．　 cos　　　 C．tan　 　D．cos2θ

解析：∵2kπ＜θ＜2kπ+(k∈Z)，

∴kπ＜＜kπ+(k∈Z)，

4kπ＜2θ＜4kπ+π(k∈Z)．

可知是第一、第三象限角，sin、cos都可能取负值，只有tan能确定为正值．

2θ是第一、第二象限角，cos2θ可能取负值．

答案：C

10.若1+sinx·+cosx·＝0，则x不可能是　　　　　　　　　　　　 (　)

A．任何象限的角

B．第一、二、三象限的角

C．第一、二、四象限的角

D．第一、三、四象限的角

解析：由已知得1+sinx·|sinx|+cosx·|cosx|＝0，

∴故x不可能是第一、二、四象限的角．

答案：C

9．(1)设90°＜α＜180°，角α的终边上一点为P(x，)，且cosα＝x，求sinα与tanα的值；

(2)已知角θ的终边上有一点P(x，－1)(x≠0)，且tanθ＝－x，求sinθ，cosθ.

解：(1)∵r＝，∴cosα＝，

从而x＝，解得x＝0或x＝±.

∵90°＜α＜180°，∴x＜0，因此x＝－.

故r＝2，sinα＝＝，

tanα＝＝－.

(2)∵θ的终边过点(x，－1)，

∴tanθ＝－，

又tanθ＝－x，∴x²＝1，∴x＝±1.

当x＝1时，sinθ＝－，cosθ＝；

当x＝－1时，sinθ＝－，cosθ＝－.

8．(2010·银川模拟)若角α的终边落在直线y＝－x上，则+的值等于　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　(　)

A．0　 　　B．2 　　　C．－2 　　　D．2tanα

解析：因为角α的终边落在直线y＝－x上，α＝kπ+，k∈Z，sinα，cosα的符号相反．当α＝2kπ+，

即角α的终边在第二象限时，sinα＞0，cosα＜0；

当α＝2kπ+，即角α的终边在第四象限时，

sinα＜0，cosα＞0.

所以有+＝+＝0.

答案：A

7．在(0,2π)内使sinx＞cosx成立的x取值范围是　　　　　　　　　　　　　 (　)

A.∪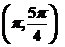　 　　　　　　　　　　B.

C.　 　　　　　　　　　　　　　　　　　　D.∪

解析：用单位圆内正弦线和余弦线来解．

答案：C

6.点P从(1,0)出发，沿单位圆x²+y²＝1逆时针方向运动弧长到达Q点，则Q的坐标为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(－，)　 　B．(－，－)　　 C．(－，－)　 　　D．(－，)

解析：根据题意得Q(cosπ，sinπ)，即Q(－，)．

答案：A

5．已知一扇形的中心角是α，所在圆的半径是R.

(1)若α＝60°，R＝10 cm，求扇形的弧所在的弓形面积；

(2)若扇形的周长是一定值c(c＞0)，当α为多少弧度时，该扇形有最大面积？

解：(1)设弧长为l，弓形面积为S_弓，

∵α＝60°＝，R＝10，∴l＝π(cm)，

S_弓＝S_扇－S_△＝×π×10－×10²×sin60°

＝50(－)(cm²)．

(2)法一：∵扇形周长c＝2R+l＝2R+αR，

∴R＝，

∴S_扇＝α·R²＝α()²＝α·

＝·≤.

∴当且仅当α＝，即α＝2(α＝－2舍去)时，扇形面积有最大值.

法二：由已知2R+l＝c，∴R＝(l＜c)，

∴S＝Rl＝··l＝(cl－l²)

＝－(l－)²+，

∴当l＝时，S_max＝，此时α＝＝＝2，

∴当扇形圆心角为2弧度时，扇形面积有最大值.

4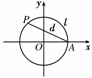．如图，设点A是单位圆上的一定点，动点P从A

出发在圆上按逆时针方向转一周，点P所旋转过

的弧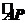的长为l，弦AP的长为d，则函数

d＝f(l)的图象大致为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

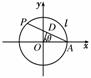解析：如图取AP的中点为D，设∠DOA=θ，则d=2sinθ，l=2θR=2θ，

∴d=2sin.

答案：C