
7.(理)给定性质:①最小正周期为π;②图象关于直线x=对称.则下列四个函数中,同时具有性质①②的是 ( )
A.y=sin(+) B.y=sin(2x+)
C.y=sin|x| D.y=sin(2x-)
解析:∵T==π,∴ω=2.对于选项D,又2×-=,所以x=为对称轴.
答案:D
6.在△ABC中,角A,B均为锐角,且cosA>sinB,则△ABC的形状是 ( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形
解析:cosA=sin(-A)>sinB,-A,B都是锐角,则-A>B,A+B<,C>.
答案:C
5.(2010·惠州模拟)将函数y=sinx的图象向左平移φ(0≤φ<2π)个单位后,得到函数y=sin(x-)的图象,则φ等于 ( )
A. B. C. D.
解析:依题意得y=sin(x-)=sin(x-+2π)=sin(x+),将y=sinx的图象向左平移个单位后得到y=sin(x+)的图象,即y=sin(x-)的图象.
答案:B
4.设a=sin15°+cos15°,b=sin17°+cos17°,则下列各式中正确的是 ( )
A.a<<b B.a<b<
C.b<<a D.b<a<
解析:a=sin(15°+45°)=sin60°,
b=sin(17°+45°)=sin62°,b>a.
=sin260°+sin262°>2sin60°sin62°=sin62°,
∴>b>a.
答案:B
3.已知sin(x+)=-,则sin2x的值等于 ( )
A.- B. C.- D.
解析:sin(x+)=(sinx+cosx)=-,
所以sinx+cosx=-,
所以(sinx+cosx)2=1+sin2x=,故sin2x=-.
答案:A
2.已知sinα=,cosα=-,且α为第二象限角,则m的允许值为( )
A.<m<6 B.-6<m< C.m=4 D.m=4或m=
解析:由sin2α+cos2α=1得,()2+(-)2=1,
∴m=4或,又sinα>0,cosα<0,把m的值代入检验得,
m=4.
答案:C
1.cos(-)-sin(-)的值是 ( )
A. B.- C.0 D.
解析:原式=cos(-4π-)-sin(-4π-)
=cos(-)-sin(-)
=cos+sin=.
答案:A
12. (2010·宁波模拟)某建筑的金属支架如图所示,根据要求
(2010·宁波模拟)某建筑的金属支架如图所示,根据要求
AB至少长2.8 m,C为AB的中点,B到D的距离比CD
的长小0.5 m,∠BCD=60°,已知建造支架的材料每米
的价格一定,问怎样设计AB,CD的长,可使建造这个
支架的成本最低?
解:设BC=am(a≥1.4),CD=bm,连接BD.
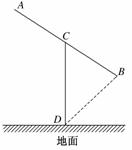 则在△CDB中,(b-)2=b2+a2-2abcos60°.
则在△CDB中,(b-)2=b2+a2-2abcos60°.
∴b=.
∴b+2a=+2a.
设t=a-1,t≥-1=0.4,
则b+2a=+2(t+1)=3t++4≥7,
等号成立时t=0.5>0.4,a=1.5,b=4.
答:当AB=3 m,CD=4 m时,建造这个支架的成本最低.
11.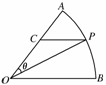 如图,扇形AOB,圆心角AOB等于60°,半径为2,
如图,扇形AOB,圆心角AOB等于60°,半径为2,
在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
解:因为CP∥OB,所以∠CPO=∠POB=60°-θ,∴∠OCP=120°.
在△POC中,由正弦定理得
=,∴=,所以CP=sinθ.
又=,∴OC=sin(60°-θ).
因此△POC的面积为
S(θ)=CP·OCsin120°=·sinθ·sin(60°-θ)×
=sinθsin(60°-θ)=sinθ(cosθ-sinθ)
=[cos(2θ-60°)-],θ∈(0°,60°).
所以当θ=30°时,S(θ)取得最大值为.
10.线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始________h后,两车的距离最小.解析:如图所示:设t h后,汽车由A行驶到D,摩托车由B行驶到E,则AD=80t,BE=50t.
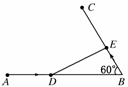 因为AB=200,所以BD=200-80t,
因为AB=200,所以BD=200-80t,
问题就是求DE最小时t的值.
由余弦定理:DE2=BD2+BE2-2BD·BEcos60°
=(200-80t)2+2500t2-(200-80t)·50t
=12900t2-42000t+40000.
当t=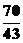 时DE最小.
时DE最小.
答案: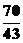
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com