17．(本小题满分12分)已知tan(α+)＝－3，α∈(0，)．

(1)求tanα的值；

(2)求sin(2α－)的值．

解：(1)由tan(α+)＝－3可得＝－3.

解得tanα＝2.

(2)由tanα＝2，α∈(0，)，可得sinα＝，cosα＝.因此sin2α＝2sinαcosα＝，cos2α＝1－2sin²α＝－，sin(2α－)＝sin2αcos－cos2αsin＝×+×＝.

16．如图是函数f(x)＝Asin(ωx+φ)(A＞0，ω＞0，－π＜φ＜π)，x∈R的部分图象，则下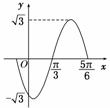列命题中，正确命题的序号为________．

①函数f(x)的最小正周期为；

②函数f(x)的振幅为2；

③函数f(x)的一条对称轴方程为x＝；

④函数f(x)的单调递增区间为[，]；

⑤函数的解析式为f(x)＝sin(2x－)．

解析：由图象可知，函数f(x)的最小正周期为(－)×2＝π，故①不正确；函数f(x)的振幅为，故②不正确；函数f(x)的一条对称轴方程为x＝＝，故③正确；④不全面，函数f(x)的单调递增区间应为[+2kπ，+2kπ]，k∈Z；由sin(2×+φ)＝得2×+φ＝+2kπ，k∈Z，即φ＝2kπ－，k∈Z，∵－π＜φ＜π，故k取0，从而φ＝－，故f(x)＝sin(2x－)．

答案：③⑤

15．在△ABC中，已知tanA＝3tanB，则tan(A－B)的最大值为________，此时角A的　　　　　　　　　　　　　　

大小为________．

解析：由于tan(A－B)＝＝＝≤.当且仅当1＝tanB时取“＝”号，则tanB＝⇒tanA＝⇒A＝60°.

答案：　60°

14．计算：＝________.

解析：＝＝＝.

答案：

13．在△ABC中，角A，B，C的对边分别为a，b，c，已知B＝60°，C＝75°，a＝4，则b＝________.

解析：易知A＝45°，由正弦定理＝得＝，解得b＝2.

答案：2

12．(2010·抚顺模拟)当0＜x＜时，函数f(x)＝的最小值为　 (　)

A．2　 　　B．2　　　 C．4 　　　　D．4

解析：f(x)＝＝＝+≥2 ＝4，当　　

且仅当＝，即tanx＝时，取“＝”，∵0＜x＜，∴存在x使tanx＝，这时f(x)_min＝4.

答案：C

11．已知函数f(x)的部分图象如图所示，则f(x)的解析

式可能为　　　　　　　　　　　　　　　 (　)

A．f(x)＝2cos(－)

B．f(x)＝cos(4x+)

C．f(x)＝2sin(－)

D．f(x)＝2sin(4x+)

解析：设函数f(x)＝Asin(ωx+φ)，由函数的最大值为2知A＝2，又由函数图象知该函数的周期T＝4×(－)＝4π，所以ω＝，将点(0,1)代入得φ＝，所以f(x)＝2sin(x+)＝2cos(x－)．

答案：A

10．已知函数f(x)＝asin2x+cos2x(a∈R)图象的一条对称轴方程为x＝，则a的值为(　)

A.　 　　　　　B.　　　　　　　　 C.　　　　　　 　D．2

解析：函数y＝sinx的对称轴方程为x＝kπ+，k∈Z，f(x)＝sin(2x+φ)，其中tanφ＝，故函数f(x) 的对称轴方程为2x+φ＝kπ+，k∈Z，而x＝是其一条对称轴方程，所以2×+φ＝kπ+，k∈Z，解得φ＝kπ+，k∈Z，故tanφ＝＝tan(kπ　

+)＝，所以a＝.

答案：C

9．在△ABC中，角A，B所对的边长为a，b，则“a＝b”是“acosA＝bcosB”的　 (　)

A．充分不必要条件　 　　　　　　　　B．必要不充分条件

C．充要条件　 　　　　　　　　　　　D．既不充分又不必要条件

解析：a＝b⇒A＝B⇒acosA＝bcosB，条件是充分的；acosA＝bcosB⇒sinAcosA＝sinBcosB⇒sin2A＝sin2B⇒2A＝2B或2A+2B＝π，即A＝B或A+B＝，故条件是不必要的．

答案：A

8．(文)如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为　　 (　)

A. 　　　B.　　　 C.　　 　D.

解析：设等腰三角形的底边为a，顶角为θ，则腰长为2a.

由余弦定理得cosθ＝＝.

答案：D

(理)△ABC的两边长分别为2,3，其夹角的余弦值为，则其外接圆的半径为(　)

A.　 　　　B.　　　 C. 　　　D．9

解析：由余弦定理得：三角形第三边长为

　 ＝3，

且第三边所对角的正弦值为 ＝，

所以2R＝⇒R＝.

答案：C