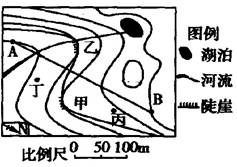
下图为某山地的局部等高线图，等高距为20米，AB为空中索道。回答1-3题。

1．乘索道上行的方向是

A．西北　　　　 B．东南

C．正北　　　　 D．正南

2．图中有一瀑布，瀑布及选择观赏的位置分别是

A．甲、乙　　　 B．丙、丁

C．丙、甲　　　 D．乙、丁

3．图中瀑布的落差不可能为

A．60米　　　 B．50米　　　 C．40米　　　 D．30米

22．(文)(本小题满分14分)已知函数y＝f(x)的图象经过坐标原点，且f(x)＝x²－x+b，数列{a_n}的前n项和S_n＝f(n)(n∈N^*)．

(1)求数列{a_n}的通项公式；

(2)若数列{b_n}满足a_n+log₃n＝log₃b_n，求数列{b_n}的前n项和T_n；

(3)设P_n＝a₁+a₄+a₇+…+a_3n－2，Q_n＝a₁₀+a₁₂+a₁₄+…+a_2n+8，其中n∈N^*，试比较P_n与Q_n的大小，并证明你的结论．

解：(1)因为y＝f(x)的图象过原点，所以f(x)＝x²－x.

所以S_n＝n²－n，

当n≥2时，a_n＝S_n－S_n－1＝n²－n－(n－1)²+(n－1)＝2n－2，

又因为a₁＝S₁＝0适合a_n＝2n－2，

所以数列{a_n}的通项公式为a_n＝2n－2(n∈N^*)．

(2)由a_n+log₃n＝log₃b_n得：b_n＝n·3a_n＝n·3^2n－2(n∈N^*)，

所以T_n＝b₁+b₂+b₃+…+b_n＝3⁰+2·3²+3·3⁴+…+n·3^2n－2，9T_n＝3²+2·3⁴+3·3⁶+…+n·3²ⁿ.

两式相减得：8T_n＝n·3²ⁿ－(1+3²+3⁴+3⁶+…+3^2n－2)＝n·3²ⁿ－，

所以T_n＝－＝.

(3)a₁，a₄，a₇，…，a_3n－2组成以0为首项，6为公差的等差数列，所以P_n＝×6＝3n²－3n；

a₁₀，a₁₂，a₁₄，…，a_2n+8组成以18为首项，4为公差的等差数列，所以Q_n＝18n+×4＝2n²+16n.

故P_n－Q_n＝3n²－3n－2n²－16n＝n²－19n＝n(n－19)，

所以，对于正整数n，当n≥20时，P_n>Q_n；

当n＝19时，P_n＝Q_n；

当n<19时，P_n<Q_n.

(理)(本小题满分14分)已知数列{a_n}的前n项和为S_n，点(a_n+2，S_n+1)在直线y＝4x－5上，其中n∈N^*.令b_n＝a_n+1－2a_n，且a₁＝1.

(1)求数列{b_n}的通项公式；

(2)若f(x)＝b₁x+b₂x²+b₃x³+…+b_nxⁿ，求f′(1)的表达式，并比较f′(1)与8n²－4n的大小．

解：(1)∵S_n+1＝4(a_n+2)－5，∴S_n+1＝4a_n+3，

∴S_n＝4a_n－1+3(n≥2)，

∴a_n+1＝4a_n－4a_n－1(n≥2)，

∴a_n+1－2a_n＝2(a_n－2a_n－1)(n≥2)，

∴＝＝2(n≥2)．

∴数列{b_n}为等比数列，其公比为q＝2，首项b₁＝a₂－2a₁，

而a₁+a₂＝4a₁+3，且a₁＝1，∴a₂＝6，

∴b₁＝6－2＝4，

∴b_n＝4×2^n－1＝2ⁿ⁺¹.

(2)∵f(x)＝b₁x+b₂x²+b₃x³+…+b_nxⁿ，

∴f′(x)＝b₁+2b₂x+3b₃x²+…+nb_nx^n－1，

∴f′(1)＝b₁+2b₂+3b₃+…+nb_n，

∴f′(1)＝2²+2·2³+3·2⁴+…+n·2ⁿ⁺¹，　　　　　　　　　　　　　　　　　　 ①

∴2f′(1)＝2³+2·2⁴+3·2⁵+…+n·2ⁿ⁺²，　　　　　　　　　　　　　　　　　　 ②

①－②得

－f′(1)＝2²+2³+2⁴+…+2ⁿ⁺¹－n·2ⁿ⁺²

＝－n·2ⁿ⁺²＝－4(1－2ⁿ)－n·2ⁿ⁺²，

∴f′(1)＝4+(n－1)·2ⁿ⁺²，

∴f′(1)－(8n²－4n)＝4(n－1)·2ⁿ－4(2n²－n－1)

＝4(n－1)[2ⁿ－(2n+1)]．

当n＝1时，f′(1)＝8n²－4n；

当n＝2时，f′(1)－(8n²－4n)＝4(4－5)＝－4<0，f′(1)<8n²－4n；

当n＝3时，f′(1)－(8n²－4n)>0，

结合指数函数y＝2^x与一次函数y＝2x+1的图象知，当x>3时，总有2^x>2x+1，

故当n≥3时，总有f′(1)>8n²－4n.

综上：当n＝1时，f′(1)＝8n²－4n；

当n＝2时，f′(1)<8n²－4n；

当n≥3时，f′(1)>8n²－4n.

21．(本小题满分12分)已知各项都不相等的等差数例{a_n}的前六项和为60，且a₆为a₁和a₂₁的等比中项．

(1)求数列{a_n}的通项公a_n及前n项和S_n；

(2)若数列{b_n}满足b_n+1－b_n＝a_n(n∈N^*)，且b₁＝3，求数列{}的前n项和T_n.

解：(1)设等差数列{a_n}的公差为d，

则解得

∴a_n＝2n+3.

S_n＝＝n(n+4)．

(2)由b_n+1－b_n＝a_n，

∴b_n－b_n－1＝a_n－1(n≥2，n∈N^*)．

当n≥2时，

b_n＝(b_n－b_n－1)+(b_n－1－b_n－2)+…+(b₂－b₁)+b₁

＝a_n－1+a_n－2+…+a₁+b₁

＝(n－1)(n－1+4)+3＝n(n+2)．

对b₁＝3也适合，

∴b_n＝n(n+2)(n∈N^*)．

∴＝＝(－)．

T_n＝(1－+－+…+－)

＝(－－)＝.

20．(本小题满分12分)已知数列{a_n}满足：a₁＝1，a₂＝，且[3+(－1)ⁿ]a_n+2－2a_n+2[(－1)ⁿ－1]＝0，n∈N^*.

(1)求a₃，a₄，a₅，a₆的值及数列{a_n}的通项公式；

(2)设b_n＝a_2n－1·a_2n，求数列{b_n}的前n项和S_n.

解：(1)经计算a₃＝3，a₄＝，a₅＝5，a₆＝.

当n为奇数时，a_n+2＝a_n+2，即数列{a_n}的奇数项成等差数列，

∴a_2n－1＝a₁+(n－1)·2＝2n－1.

当n为偶数时，a_n+2＝a_n，即数列{a_n}的偶数项成等比数列，

∴a_2n＝a₂·()^n－1＝()ⁿ.

因此，数列{a_n}的通项公式为a_n＝

(2)∵b_n＝(2n－1)·()ⁿ，

∴S_n＝1·+3·()²+5·()³+…+(2n－3)·()^n－1+(2n－1)·()ⁿ，　　　　　　　　　 ①

S_n＝1·()²+3·()³+5·()⁴+…+(2n－3)·()ⁿ+(2n－1)·()ⁿ⁺¹，　　　　　　　　　 ②

①②两式相减，

得S_n＝1·+2[()²+()³+…+()ⁿ]－(2n－1)·()ⁿ⁺¹

＝+－(2n－1)·()ⁿ⁺¹

＝－(2n+3)·()ⁿ⁺¹.

∴S_n＝3－(2n+3)·()ⁿ.

19．(本小题满分12分)(2010·黄冈模拟)已知二次函数f(x)＝x²－ax+a(a≠0)，不等式f(x)≤0的解集有且只有一个元素，设数列{a_n}的前n项和为S_n＝f(n)．

(1)求数列{a_n}的通项公式；

(2)设各项均不为0的数列{c_n}中，满足c_i·c_i+1<0的正整数i的个数称作数列{c_n}的变号数，令c_n＝1－(n∈N^*)，求数列{c_n}的变号数．

解：(1)由于不等式f(x)≤0的解集有且只有一个元素，

∴Δ＝a²－4a＝0⇒a＝4，

故f(x)＝x²－4x+4.

由题S_n＝n²－4n+4＝(n－2)²

则n＝1时，a₁＝S₁＝1；

n≥2时，a_n＝S_n－S_n－1＝(n－2)²－(n－3)²＝2n－5，

故a_n＝

(2)由题可得，c_n＝.

由c₁＝－3，c₂＝5，c₃＝－3，

所以i＝1，i＝2都满足c_i·c_i+1<0，

当n≥3时，c_n+1>c_n，且c₄＝－，

同时1－>0⇒n≥5，

可知i＝4满足c_i、c_i+1<0，n≥5时，均有c_nc_n+1>0.

∴满足c_ic_i+1<0的正整数i＝1,2,4，故数列{c_n}的变号数为3.

18．(本小题满分12分)设数列{a_n}满足a₁＝t，a₂＝t²，前n项和为S_n，且S_n+2－(t+1)S_n+1+tS_n＝0(n∈N^*)．

(1)证明数列{a_n}为等比数列，并求{a_n}的通项公式；

(2)当<t<2时，比较2ⁿ+2^－n与tⁿ+t^－n的大小；

(3)若<t<2，b_n＝，求证：++…+<2ⁿ－2－.

解：(1)证明：由S_n+2－(t+1)S_n+1+tS_n＝0，得tS_n+1－tS_n＝S_n+2－S_n+1，即a_n+2＝ta_n+1，

而a₁＝t，a₂＝t²，∴数列{a_n}是以t为首项，t为公比的等比数列，

∴a_n＝tⁿ.

(2)∵(tⁿ+t^－n)－(2ⁿ+2^－n)＝(tⁿ－2ⁿ)[1－()ⁿ]，又<t<2，∴<<1，则tⁿ－2ⁿ<0且1－()ⁿ>0，

∴(tⁿ－2ⁿ)[1－()ⁿ]<0，∴tⁿ+t^－n<2ⁿ+2^－n.

(3)证明：∵＝(tⁿ+t^－n)，

∴2(++…+)<(2+2²+…2ⁿ)+(2^－1+2^－2+…+2^－n)＝2(2ⁿ－1)+1－2^－n＝2ⁿ⁺¹－(1+2^－n)<2ⁿ⁺¹－2，

∴++…+<2ⁿ－2－.

17．(本小题满分12分)已知数列{a_n}中，其前n项和为S_n，且n，a_n，S_n成等差数列(n∈N^*)．

(1)求数列{a_n}的通项公式；

(2)求S_n>57时n的取值范围．

解：(1)∵n，a_n，S_n成等差数列，

∴S_n＝2a_n－n，S_n－1＝2a_n－1－(n－1)　(n≥2)，

∴a_n＝S_n－S_n－1＝2a_n－2a_n－1－1　(n≥2)，

∴a_n＝2a_n－1+1　(n≥2)，

两边加1得a_n+1＝2(a_n－1+1)　(n≥2)，

∴＝2　(n≥2)．

又由S_n＝2a_n－n得a₁＝1.

∴数列{a_n+1}是首项为2，公比为2的等比数列，

∴a_n+1＝2·2^n－1，即数列{a_n}的通项公式为a_n＝2ⁿ－1.

(2)由(1)知，S_n＝2a_n－n＝2ⁿ⁺¹－2－n，

∴S_n+1－S_n＝2ⁿ⁺²－2－(n+1)－(2ⁿ⁺¹－2－n)

＝2ⁿ⁺¹－1>0，

∴S_n+1>S_n，{S_n}为递增数列．

由题设，S_n>57，即2ⁿ⁺¹－n>59.

又当n＝5时，2⁶－5＝59，∴n>5.

∴当S_n>57时，n的取值范围为n≥6(n∈N^*)．

16．(文)将全体正整数排成一个三角形数阵：

1

2　3

4　5　6

7　8　 9　10

11　12　13　14　15

…　…　…　…　…　…

根据以上排列规律，数阵中第n(n≥3)行的从左至右的第3个数是________．

解析：前n－1行共有正整数1+2+…+(n－1)＝个，即个，

因此第n行第3个数是全体正整数中第+3个，

即为.

答案：

(理)下面给出一个“直角三角形数阵”：

，

，，

…

满足每一列的数成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i行第j列的数为a_ij(i≥j，i，j∈N^*)，则a₈₃＝________.

解析：由题意知，a₈₃位于第8行第3列，且第1列的公差等于，每一行的公比都等于.由等差数列的通项公式知，第8行第1个数为+(8－1)×＝2，a₈₃＝2×()²＝.

答案：

15．已知等差数列{a_n}的首项a₁及公差d都是整数，前n项和为S_n(n∈N^*)．若a₁>1，a₄>3，S₃≤9，则通项公式a_n＝________.

解析：由a₁>1，a₄>3，S₃≤9得，，令x＝a₁，y＝d得，，在平面直角坐标系中作出可行域可知符合要求的整数点只有(2,1)，即a₁＝2，d＝1，所以a_n＝2+n－1＝n+1.

答案：n+1

14．已知数列{a_n}满足a₁＝，a_n＝a_n－1+(n≥2)，则{a_n}的通项公式为________．

解析：a_n－a_n－1＝＝(－)，a_n＝(a_n－a_n－1)+(a_n－1－a_n－2)+…+(a₂－a₁)+a₁＝(－+－+…+1－+1)，得：a_n＝－.

答案：a_n＝－