6．已知等差数列的第k,n,p项构成等比数列的连续3项，如果这个等差数列不是常数列，则等比数列的公比为

?　 A．?　　　 B．　　　　　 C．　　　　 D．

5．如果数列{}的前n项和,那么这个数列的通项公式是　

?A．=2(n+n+1)?　　　　　　　　　 B．=3·2

?C．=3n+1?　　　　　　　　　　　 D．=2·3

4．实数等比数列{}，＝，则数列{}中　

?A．任意一项都不为零　　　　　　　 ?B．必有一项为零

?C．至多有有限项为零　　　　　　　　 D．可以有无数项为零

3．已知等比数列{}中，=2×3,则由此数列的偶数项所组成的新数列的前n项和的值为

?　 A．3－1?　　　　　　　　　 B．3(3－1)?　　　

　　 C．?　　　　　　　　　 D．

2．已知数列{}的前n项和=3－2,那么下面结论正确的是　

?A．此数列为等差数列　　　　　　　 ?B．此数列为等比数列

?C．此数列从第二项起是等比数列　　　 D．此数列从第二项起是等差数列

1．已知数列{}既是等差数列又是等比数列，则这个数列的前n项和为

A．0　　　　　 ?　　　　　　　　　 B．n 　　　　　?

C．n a　　　　 ?　　　　　　　　　 D．a

16．(2010山东德州)粉笔是校园中最常见的必备品．图1是一盒刚打开的六角形粉笔，总支数为50支．图2是它的横截面(矩形ABCD)，已知每支粉笔的直径为12mm，由此估算矩形ABCD的周长约为_______ mm．(，结果精确到1 mm)

[关键词]正六边形特点、密铺

[答案]300

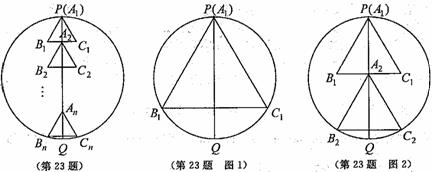
23．(2010浙江省喜嘉兴市)如图，已知⊙O的半径为1，PQ是⊙O的直径，n个相同的正三角形沿PQ排成一列，所有正三角形都关于PQ对称，其中第一个△A₁B₁C₁的顶点A₁与点P重合，第二个△A₂B₂C₂的顶点A₂是B₁C₁与PQ的交点，…，最后一个△A_nB_nC_n的顶点B_n、C_n在圆上．

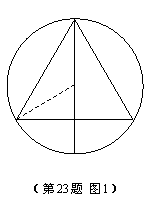
(1)如图1，当n＝1时，求正三角形的边长a₁；

(2)如图2，当n＝2时，求正三角形的边长a₂；

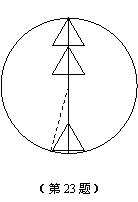
(3)如题图，求正三角形的边长a_n (用含n的代数式表示)．

[关键词]圆、正三角形、勾股定理

[答案](1)设与交于点D，连结，

则，

在中，，

即，

解得．　 …4分

(2)设与交于点E，连结，

则，

在中，

即，

解得． 　　…4分

(3)设与交于点F，连结，

则，

在中，

即，

解得． 　　…4分

11．(2010年安徽省芜湖市)一个正多边形的每个外角都是36°，这个正多边形的边数是__________．

[关键词]正多边形的外角和公式

[答案]十

1、(2010年宁波市)如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若，。

(1)求⊙O的半径;

(2)求图中阴影部分的面积。

[关键词]垂径定理，扇形面积

[答案]

解：(1)∵直径AB⊥DE

　　　　　　 ∴

　　　　　　 ∵DE平分AO

　　　　　　 ∴

　　　　　　 又∵

　　　　　　 ∴

　　　　　　 在Rt△COE中，

　　　　　　 ∴⊙O的半径为2。

　　　　　 (2)连结OF

　　　　　　　　 在Rt△DCP中，∵

　　　　　　　　 ∴

　　　　　　　　 ∴

　　　　　　　　 ∵